Can You Solve This Infinite Sum Puzzle? Let's Find Out!
Written on
Chapter 1: The Infinite Sum Challenge
Here’s a captivating algebra puzzle that intricately weaves together logarithms and the concept of an infinite series. The task at hand is to skillfully rearrange each term to reach our target format.
Are you clever enough to tackle it? I suggest pausing for a moment, grabbing your pen and paper, and giving this a shot. Once you're prepared, continue reading for the solution!
The first video titled "Finding The Sum of an Infinite Geometric Series" delves into the methods and techniques required to solve such puzzles. It will provide you with valuable insights that may aid in your understanding.
Solution
The core of this puzzle lies in the following property:
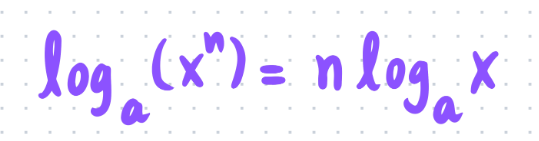
We can bring down the exponent of n to the front of the logarithm. In our scenario, we will move 0.3, 0.3², 0.3³, and so forth, to the front like this:
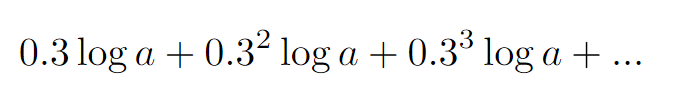
Each term contains log(a), so let's factor that out:
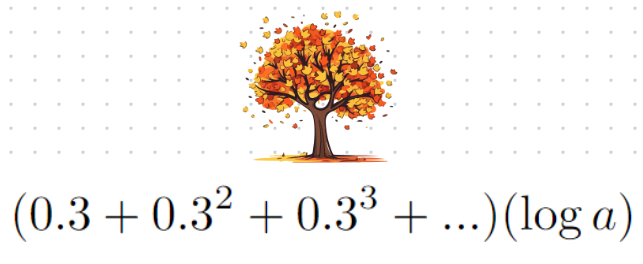
Now, our task is to evaluate the infinite sum with a common ratio of 0.3. Given that 0.3 is less than 1, we can utilize the formula S = a/(1 - r).
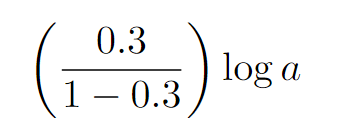
In this case, both the initial term a and the common ratio r are 0.3. We can now simplify our expression, leading us to our final answer.

Photo by Demi-Felicia Vares on Unsplash
Isn’t that fascinating?
What was your thought process while working through this? I’d love to hear your insights in the comments below!
Chapter 2: Explore More Math Puzzles
The second video titled "Can You Find the Sum of the Infinite Series? | Learn How!" explores various approaches to tackling infinite series problems. It's a great resource to deepen your understanding!
Feel free to share the following collection of intriguing math puzzles with your friends:
Math Puzzles
The finest math puzzles across Medium, covering Algebra, Geometry, Calculus, Number Theory, and more.
Bella’s Weekly Math Games
Join a thrilling 48-hour math competition every week!
Thank you for taking the time to read this! If you found the article helpful, please give it a clap.

Should you feel inclined, I would greatly appreciate any support for my writing endeavors. Your contributions help sustain my academic and personal journey.
Happy Solving, Bella!
If you'd like to connect or chat, feel free to reach out!