Essential Dimensionality Reduction Techniques for Data Science
Written on
Understanding Dimensionality in Data
In the realms of Statistics and Machine Learning, the term "dimensionality" refers to the number of attributes, features, or input variables within a dataset. For instance, consider a straightforward dataset with two features: Height and Weight. This dataset is two-dimensional, allowing each observation to be represented on a 2D graph.

Imagine enhancing this dataset by adding a third dimension, Age. This action transforms it into a three-dimensional dataset, where each observation now exists in a 3D space.
Real-world datasets often contain numerous attributes, placing their observations in high-dimensional spaces that are challenging to visualize. In a tabular dataset, each column signifies a dimension within the n-dimensional feature space, while the rows represent data points within that space.
Dimensionality reduction is a technique aimed at decreasing the number of attributes in a dataset while preserving as much variability as possible from the original dataset. This preprocessing step is crucial before model training. This article will delve into 11 key dimensionality reduction techniques and demonstrate their application using Python and Scikit-learn libraries.
The Significance of Dimensionality Reduction
When we perform dimensionality reduction, there is often a minor loss of variability—typically between 1% and 15%, depending on how many components or features we retain. However, this slight loss is outweighed by the numerous advantages of dimensionality reduction:
- Reduced Training Time: Fewer dimensions lead to quicker training times and lower computational resource requirements, enhancing the overall efficiency of machine learning algorithms.
- Mitigating the Curse of Dimensionality: In high-dimensional datasets, data points tend to cluster near the edges of the space, making effective training challenging. This phenomenon is known as the curse of dimensionality, a technical term that can be ignored for practical purposes.
- Preventing Overfitting: A high number of features increases model complexity, often leading to overfitting on training data. Dimensionality reduction helps simplify models.
- Facilitating Data Visualization: Lower-dimensional data can be plotted easily in 2D or 3D, aiding in visual analysis.
- Addressing Multicollinearity: In regression analysis, multicollinearity occurs when independent variables are highly correlated. Dimensionality reduction consolidates these correlated variables into uncorrelated sets, resolving multicollinearity issues.
- Improving Factor Analysis: This technique helps identify latent variables that are inferred from other dataset variables.
- Noise Reduction: By retaining only the most significant features and discarding redundant ones, dimensionality reduction decreases noise, enhancing model accuracy.
- Image Compression: This technique minimizes image file size while maintaining quality, with pixels serving as dimensions of image data.
- Transforming Non-linear Data: Techniques like Kernel PCA can convert non-linear datasets into linearly separable forms.
Dimensionality Reduction Techniques
Numerous dimensionality reduction methods exist, each suited for different data types and requirements. These methods can be categorized into two primary types: feature selection methods and transformation methods.
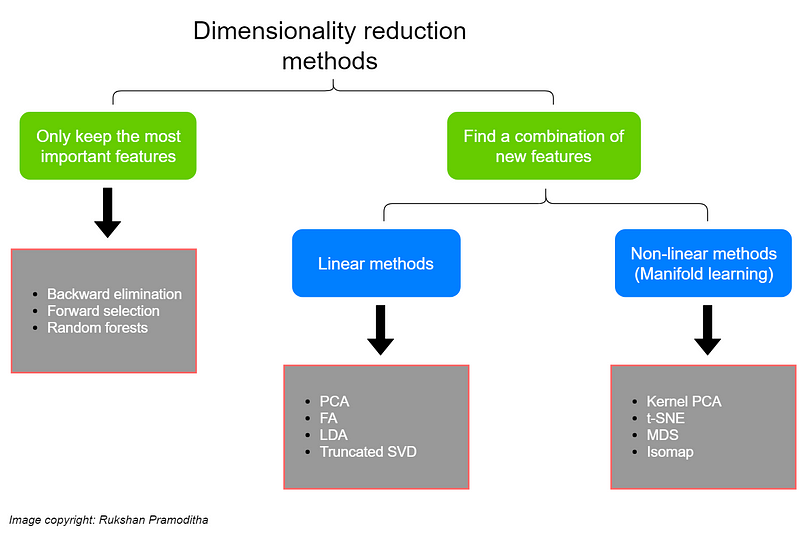
Feature Selection Methods
These methods focus on retaining the most important features while discarding redundant ones without applying transformations.
- Backward Elimination
- Forward Selection
- Random Forests
Transformation Methods
These methods create new feature combinations through transformations. They can be further divided into linear and non-linear methods:
#### Linear Methods
These methods project original data linearly onto a lower-dimensional space. Examples include:
- Principal Component Analysis (PCA)
- Factor Analysis (FA)
- Linear Discriminant Analysis (LDA)
- Truncated Singular Value Decomposition (SVD)
#### Non-linear Methods
For non-linear datasets, these methods can effectively reduce dimensionality:
- Kernel PCA
- t-Distributed Stochastic Neighbor Embedding (t-SNE)
- Multidimensional Scaling (MDS)
- Isometric Mapping (Isomap)
Let's explore each method in more detail. For PCA and FA, I will reference previous works that elaborate on their theory and implementation.
Linear Methods
Principal Component Analysis (PCA)
PCA is a favorite among machine learning practitioners. It transforms correlated variables into a smaller number of uncorrelated variables, known as principal components, while retaining as much variability as possible.
Factor Analysis (FA)
Unlike PCA, which primarily focuses on dimensionality reduction, FA aims to identify latent variables inferred from other dataset variables.
Linear Discriminant Analysis (LDA)
Typically used for multi-class classification, LDA also serves as a dimensionality reduction technique by optimizing class separability through linear combinations of input features.
Truncated Singular Value Decomposition (SVD)
This method effectively reduces dimensionality for sparse datasets, contrasting with PCA, which is more suitable for dense data.
Non-linear Methods
Kernel PCA
This technique applies kernel functions to project data into a higher-dimensional space, facilitating linear separability.
Vishal Patel | A Practical Guide to Dimensionality Reduction Techniques - YouTube
Kernel PCA is especially useful for non-linear datasets. It temporarily transforms the data into a higher-dimensional space before projecting it back to a lower dimension.
t-Distributed Stochastic Neighbor Embedding (t-SNE)
This method excels in visualizing high-dimensional data, particularly for image processing and natural language processing tasks.
Dimensionality Reduction Tutorial 4 Video 1 - YouTube
Multidimensional Scaling (MDS)
MDS preserves inter-instance distances during dimensionality reduction, with options for metric and non-metric algorithms.
Isometric Mapping (Isomap)
This method extends MDS and Kernel PCA by calculating geodesic distances among nearest neighbors.
Other Feature Selection Techniques
These methods focus on retaining significant features while discarding redundant ones, inadvertently performing dimensionality reduction in the process.
- Backward Elimination
- Forward Selection
- Random Forests
This concludes the overview of essential dimensionality reduction techniques. Embracing these methods will enhance your data analysis and machine learning capabilities.
Happy learning, and see you in the next discussion!