Chapter 1: The Concept of Virtual Particles

Virtual particles, which may be understood as real particles that are out of sync with our observable universe, are a fascinating topic in physics.

Isaac Newton's introduction of the term "force" laid the groundwork for modern physics. While most forces manifest between tangible objects, the concept of virtual particles adds depth to our understanding of forces. Some argue that virtual particles are merely a byproduct of our calculations, while others view them as fleeting states of fields. In this discussion, I will explore how a five-dimensional theory might reinterpret these particles as being "out of phase" with our four-dimensional reality.

The majority of everyday forces we encounter are electromagnetic in nature. For instance, when I press my hand against a wall, the electromagnetic forces binding the electrons of my hand to their respective atoms, as well as those within the wall, resist my push. Thus, it can be said that I never truly "touch" anything.

Classical physicists correlated Newton's notion of force with the universal principle of energy. Forces arise because all systems—be it a block on an inclined plane or a weight on a pulley—are striving toward a lower energy state, or ground state. The interplay of forces leads to changes in speed, indicating an exchange between potential and kinetic energy.

In classical physics, fields are responsible for mediating forces. A positive charge generates an electric field that affects negative charges, drawing them closer together. Their ground state ideally involves them occupying the same space, though other forces may prevent this, as seen in bosons.

Quantum physics shifted the paradigm from a force field concept to a particle field framework (or more accurately, wave packets). The interaction between a magnet and an iron object occurs through the exchange of bosons—specifically, photons. Although these photons are not directly observable, they facilitate a reduction in energy as the magnet and iron come closer together. The pivotal realization that force-carrying boson exchanges underlie these interactions marked a significant milestone in mid-20th-century physics.

However, a crucial point of contention is that the photons involved in electromagnetic interactions are actually not real particles. They manifest as virtual particles that elude direct observation.

Richard Feynman is credited with coining the term "particles" for these entities, although they could just as easily be termed field excitations. His diagrams, known as Feynman diagrams, represent force interactions as particle exchanges, a concept arising from perturbation theory—a mathematical technique that simplifies calculations by focusing on significant effects.

The characterization of virtual particles as such is contentious. Their amplitudes are imaginary, and they do not conform to the typical mass, momentum, and energy relationships. They are described as "off mass shell," leading to the notion that they exist as computational entities rather than physical ones.

Despite the challenges in asserting their existence due to their indirect measurability, they cannot be outright dismissed—unlike ghost particles, which are purely computational constructs.

In a recent paper I published in Physical Review D, I revisited the notion of virtual particles. I employed the classical interpretation of quantum theory within four dimensions of space and time, coupled with an additional dimension. Under this framework, virtual particles become non-existent, as classical physics demands clear inputs and outputs for every interaction. Feynman diagrams, which resemble tree structures with numerous particles interacting and producing new particles, lack the loops indicative of virtual particle exchanges found in quantum mechanics.

To transition from a five-dimensional classical universe to a four-dimensional quantum one, one averages over the fifth dimension. When particle interactions are averaged in this manner, virtual particles emerge as loops that represent statistical correlations, linking inputs to outputs.

If we consider the universe as five-dimensional, virtual particles become "real" in the sense that they are not merely loops. Nevertheless, they retain their imaginary amplitudes when they are off mass shell. The 5-D approach resolves this issue through a mathematical technique known as Wick rotation, which transforms time into imaginary time, rendering all particles entirely real. Calculations proceed in this imaginary context, and upon obtaining results, one reverts to actual time.

However, this raises a question: if a 5-D universe only appears sensible with imaginary time, can we accept the fifth dimension as real?

Interestingly, various domains utilize imaginary numbers to model tangible phenomena, especially in wave-related contexts. Imaginary and complex numbers (a combination of real and imaginary values) prove invaluable in describing wave behavior.

Mathematically, a pure wave is defined by three parameters: amplitude (the wave's height), frequency (how often the wave oscillates), and phase (the wave's offset relative to another).

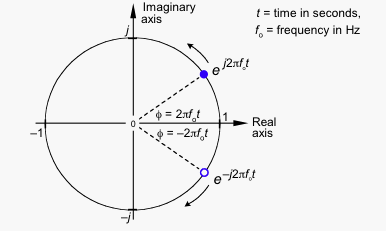
A complex number can be characterized by its magnitude and direction, correlating to amplitude and phase. The intriguing aspect arises when a complex number is rotated around a circle in the complex plane at a steady rate, establishing a frequency while maintaining a constant radius. This becomes pivotal when combining pure tones to generate intricate waveforms.

This can also be illustrated through digital signals. Sound and other signals are often digitized by sampling or synthesizing data at 90-degree phase offsets. These in-phase and quadrature (I/Q) components correspond to the real and imaginary parts of the signal. With rapid sampling, one can reproduce sound or signals with precise amplitude and phase. Without the quadrature data, crucial phase information would be lost.

If voice can be represented as complex numbers, then it stands to reason that reality can be too.

In quantum physics, amplitude signifies the likelihood of an event, such as the appearance of a particle in a specific location. However, what do frequency and phase represent? In classical wave theory, phase and frequency relate to orientation and configuration in space and time.

In quantum mechanics, these waves orient within a space called configuration space, encompassing all potential arrangements of field sets. In conventional theory, these configurations are superimposed, forming a single expansive wave that embodies all possible realities. These realities interact similarly to actual waves, with phase and frequency dictating their constructive or destructive interference.

In the context of a 5-D theory, these configurations evolve stochastically with random noise in a fifth dimension, rather than existing in superposition. They propagate as complex, sometimes chaotic waves through the fifth dimension.

In my research, I demonstrated that a simple 5-D wave of massive particles remains "on mass shell" in five dimensions. However, it only aligns in four dimensions if its fifth-dimensional momentum is constant, meaning that all momentum, minus a fixed value, resides within a four-dimensional slice. These represent the "real" particles we observe, possibly because only these waves constructively interfere within our slice, thus maintaining their existence in our universe.

From this analysis, it is evident that virtual particles possess two key traits: they are off mass shell, likely due to being out of phase with our 4-D reality, and they impact real particles through their statistical properties.

Consequently, virtual particles are just as legitimate as "real" particles. They exist as waves within the fifth dimension, but their out-of-phase nature leads to destructive interference, preventing their manifestation within our observable universe.

This phenomenon doesn't affect predictions until we incorporate gravity. As both a force carrier and a theory of space-time, gravity must include "virtual" particles, or gravitons, thus establishing a five-dimensional spacetime. How is this feasible?

The answer lies in the necessity for symmetry breaking to achieve this. One must decompose the 5-D framework into three components: a gravity force carrier functioning as the metric of our 4-D spacetime, along with a vector force carrier (akin to electromagnetism) and a scalar force carrier (such as the Higgs field). While the latter two remain unmeasured, they are integral to relativistic MOND-style dark matter theories, suggesting we may be detecting their effects presently.

This implies that gravitons could exist in three distinct varieties, all propagating virtual particles through the fifth dimension.

If it can be demonstrated that this 5-D theory can elucidate our observations of dark matter and potentially dark energy, it would lend substantial support to the validity of the theory.

References

Andersen, Timothy D. “Quantization of fields by averaging classical evolution equations.” Physical Review D 99.1 (2019): 016012.

Andersen, Timothy D. “Chaotic deterministic quantization in a 5D general relativity.” arXiv preprint arXiv:2110.05180 (2021).

Chapter 2: Understanding Virtual Particles

The concept of virtual particles is further explored in the following videos:

This video, titled "Can Something Come From Nothing? Virtual Particles," delves into the nature of virtual particles and their implications in quantum physics.

The second video, "What are virtual particles?", provides a comprehensive overview of virtual particles and their role in modern physics.