Section 1.1: Why is Quantum Gravity Important?

One of the most profound mysteries in physics is the existence of the graviton, the particle thought to mediate gravitational force within a quantum framework. But what leads us to believe in the existence of the graviton? The Standard Model of particles predicts 13 particles, and with the first 12 confirmed, scientists hypothesize that the 13th, the graviton, must also exist.

Moreover, while general relativity has been remarkably successful, it is not considered fundamental. It fails to delve into the finer aspects of the fundamental constituents of our universe, such as electrons, quarks, and photons, which have all been confirmed experimentally. Thus, there is a strong argument for the existence of a quantum theory of gravity.

The pressing need for a quantum gravity model stems from the fact that while the other three fundamental forces—electromagnetic, weak, and strong interactions—are well described by quantum field theories, gravity lacks a comparable quantum field framework. It is commonly stated that one cannot adequately couple a classical system with a quantum one.

Section 1.2: Expected Properties of the Graviton

If the graviton exists, it is expected to be massless, propagating at the speed of light, much like photons. However, let’s consider a hypothetical scenario where we know the mass of the graviton. We can express its de Broglie-Compton mass using the following equation:

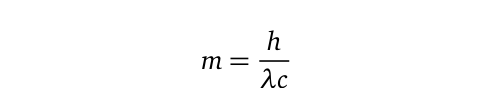
Where (h) represents Planck's constant, (lambda) is its wavelength, and (c) denotes the speed of light in a vacuum. To find the field force exerted by a single graviton on spacetime, we can multiply both sides by Newtonian gravitational acceleration (g):

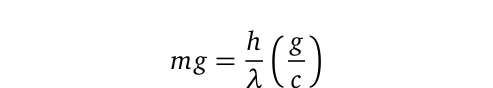
The term in the brackets on the right-hand side (RHS) of the equation can be characterized as a constant, derived from general relativistic calculations. In general, the ratio (g/c) for a sufficiently large object can be expressed as:

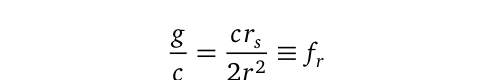
Where (r_s) is the Schwarzschild radius, and (r) is the object's radius. This equation applies to all entities, from everyday objects to planets, neutron stars, and black holes—except for the case of black holes where (r=r_s). A more detailed discussion about the derivation of this equation can be found in a separate article on extending Einstein's field equations.

What’s particularly intriguing is that this ratio yields units of per second, or frequency, which we will denote as (f_g). Rewriting the earlier equation based on this premise leads us to an expression for the energy component:

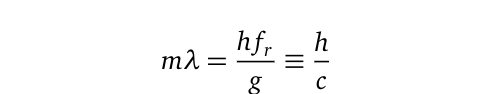
The general Planck-Einstein relation concerning the photoelectric effect of light-matter interaction is given by (E=hf). Thus, we can substitute this into the earlier equation to arrive at the graviton wave-energy as (E=hf_g). Since we have all the necessary components of the earlier equation, we can easily estimate the particle’s frequency (f_g). The particle’s wavelength (lambda) can also be derived from the relationships:

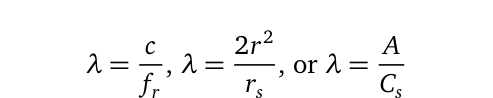
Where (c), (r), (r_s), and (f_g) retain their previous definitions. For spherical objects, (A) represents the surface area, defined as (A=4pi r^2), while (C_g) is the circumference based on the Schwarzschild radius, (C_g=2pi r_s). Although this equation applies universally, our primary concern lies with objects relevant to Earth.

Next, we can determine the particle’s wave momentum as follows:

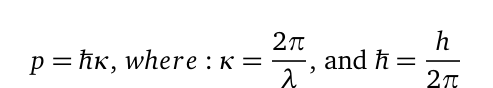
Here, (k) is the wave number, representing spatial frequency, and (hbar) is the reduced Planck's constant. Finally, we will employ the complete version of (E=mc^2):

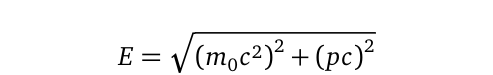
With all components of this equation known, except for the rest mass (m_g), we can proceed to solve for it. One might expect that the rest mass would resolve to zero, but that is not the case. Instead, our analysis suggests that the graviton can be characterized by a miniature mass-energy of approximately (1.35364 times 10^{-22} , text{eV/c}^2) and an even smaller rest mass (m_g) of (4.66 times 10^{-24} , text{eV/c}^2). While this methodology may appear straightforward, understanding the underlying functions is essential, as they are consistently verifiable.

Moreover, it is noteworthy that the LIGO/Virgo team in 2016 estimated the relativistic mass of gravitational waves observed from a binary black hole merger to be about (1.22 times 10^{-22} , text{eV/c}^2), citing uncertainties in their measured Compton wavelength. This correlation suggests a close relationship between our derived values and previous predictions.