The Fundamentals

Defining an imaginary number is straightforward. We can express i as follows:

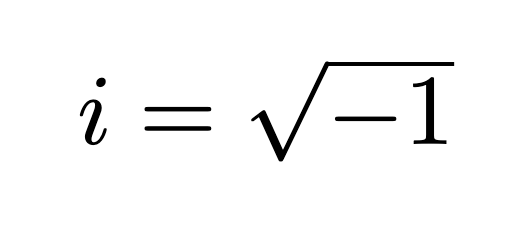
Complex numbers, which include imaginary numbers, can be generally represented as a + b*i*. Any number that incorporates i is classified as imaginary, and this broader definition encompasses all possible imaginary numbers. While high school math may suggest that negative numbers lack square roots, this changes when we consider complex numbers. For instance:

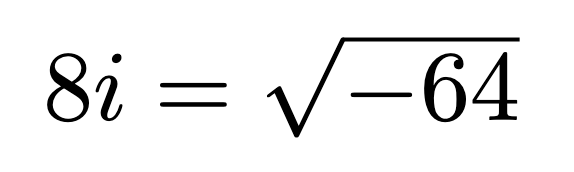
Embracing this concept opens up numerous possibilities, enabling a plethora of equations that rely on i. This leads us to the complex number plane, which features both a real axis and an imaginary axis.

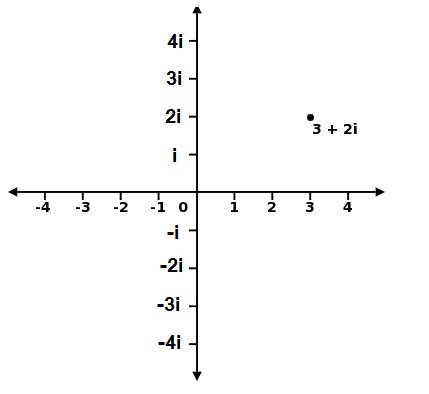
Real numbers can also be plotted on this plane, strictly along the x-axis, while each imaginary number corresponds to a point in this two-dimensional space.

Imaginary numbers have a rich history, first recorded in the 1500s by mathematician Gerolamo Cardano, who encountered them while attempting to solve cubic equations. He noted the necessity of working with square roots of negative numbers, yet referred to them as "as subtle as they are useless."

For centuries, this sentiment persisted among mathematicians. While some found them useful for specific problems, they were often regarded as bothersome. René Descartes famously remarked in 1637 that these numbers were "sometimes only imaginary," suggesting they lacked tangible existence.

Consider this equation:

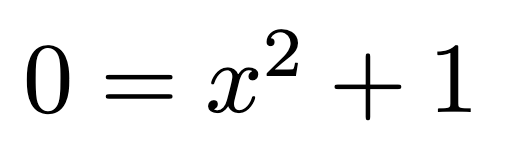
Without imaginary numbers, solving it would be unfeasible. However, with their introduction, solutions become readily apparent:

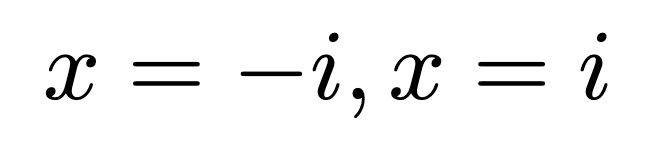
Despite skepticism, mathematicians continued to utilize imaginary numbers. It was Gauss who first acknowledged their value, recognizing them as vital tools in mathematics. In wave theory, a single imaginary number can encapsulate both amplitude and frequency, making them indispensable in fields like physics and electrical engineering.

But Are They Real?

We have examined various applications of complex or imaginary numbers, but does that suffice to classify them as real? To address this, we must first understand what "real" means in the context of numbers. Natural numbers, the most fundamental type, consist of counting numbers like 1, 2, and 100. Conversely, numbers like -10, 5/7, and 0 do not qualify.

Natural numbers are widely accepted as real, serving to quantify the size of sets. This fundamental task ranges from counting apples to assessing national populations.

Yet, we also engage with other numerical frameworks. By extending natural numbers to integers, we include negative numbers and zero, introducing more complexity. For instance, one cannot have -2 apples, but integers allow for comparative statements, such as one bowl having two fewer apples than another.

Though these distinctions may seem trivial, early mathematical literature often dismissed negative numbers as nonsensical. Gradually, their practical applications, particularly in representing debts, led to broader acceptance by the 1800s. The concept of zero also underwent a lengthy acceptance process, albeit shorter than that of negative numbers.

Beyond natural numbers and integers, fractions offer a different perspective, representing ratios between sets—a concept distinct from both natural numbers and integers. Rational numbers and irrational numbers, such as pi and the square root of 2, further diversify our understanding of numbers.

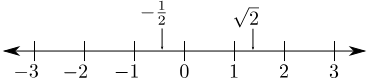
Collectively, these concepts form what we refer to as "real" numbers, encompassing a spectrum of definitions, from simple counting to continuous measurements like lengths.

Technically, imaginary numbers do not belong to the category of real numbers, as they fall outside the four classifications discussed. Nevertheless, I contend that they constitute a genuine part of our reality, exhibiting clear applications and adhering to consistent mathematical rules.

The accompanying image illustrates the various classifications I've outlined, showcasing examples of each type. While natural numbers fit within integers, which in turn fall under fractions (or rational numbers), irrational numbers remain separate. Imaginary numbers, although distinct, belong to a broader category that I propose to label as numbers pertaining to reality.

Perhaps the term "imaginary" suffers from a branding issue, leading to its exclusion from the category of "real" numbers.

What are your thoughts? I welcome your insights in the comments!

Exploring Further

I hope you found this discussion enlightening! Imaginary numbers are fascinating, and their applications are remarkable. Understanding the evolution of different number types can be intriguing, especially as imaginary numbers navigate a similar journey. If you're keen to learn more, I've compiled some resources to kickstart your exploration:

• This free online algebra book offers a solid overview of complex numbers and their applications. For a more comprehensive textbook, consider this one (also free).
• The history of mathematics is rich with intriguing narratives, many of which once seemed absurd. For a broad overview, check out the Wikipedia page on the history of math.
• This resource delves deeply into the topic, offering insights beyond what I covered here.
• This article features engaging visuals related to imaginary numbers and expands on the arguments presented in this discussion.
• I recommend this page, which intuitively explains imaginary numbers and their applications in quantum mechanics!

Additionally, I have similar articles that you may find interesting. Feel free to explore them!

<div class="link-block">

<div>

<div>

<h2>The Wild Worlds of Geometry</h2>

<div><h3>Revisiting the basics can lead to all sorts of new discoveries</h3></div>

<div><p>www.cantorsparadise.com</p></div>

</div>

</div>

</div>

<div class="link-block">

<div>

<div>

<h2>What is Graph Theory?</h2>

<div><h3>A deep dive into how one of the most important areas of mathematics started with a fun puzzle!</h3></div>

<div><p>www.cantorsparadise.com</p></div>

</div>

</div>

</div>

If you enjoyed this article, consider giving it a clap! You might also want to follow me for more content or subscribe to my email list, as I share weekly insights on math and science.