Chapter 1: The Hamiltonian Framework

In the preceding discussion, I explored the Hamiltonian associated with a gas of electrons. This Hamiltonian comprises three components: potential energy, kinetic energy, and self-interaction energy. Among these, the potential energy incorporates an external potential term, represented as ( v ) in the following equation.

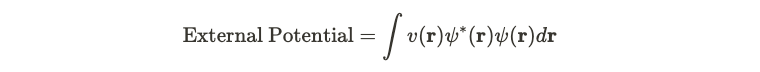
Every quantum system has a defined ground state, which is the configuration with the lowest possible energy. From this ground state, we can derive several intriguing quantities. One of these is the anticipated number of particles present in the ground state. In quantum field theory, a specific operator—commonly referred to as the ‘number operator’—is employed to ascertain this density. This operator is a function of both the creation operator and the annihilation operator.

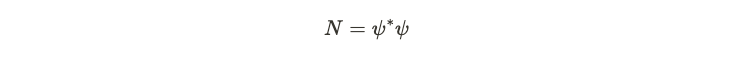
However, in this context, the interpretation diverges somewhat. Since we are examining a gas of electrons, we derive a value that signifies the expected electron density at a specific position. Thus, a higher value at a certain location ( r ) indicates a greater anticipated density of electrons. In the referenced paper [1], this electron density is denoted as ( n ).

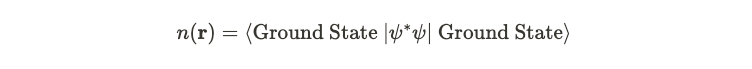
Chapter 2: Establishing Relationships

What is the connection between the electron density function and the external potential? Interestingly, a one-to-one correspondence exists between these two aspects. This principle is one of the foundational proofs presented in the paper. If we consider a different external potential ( v' ), it cannot produce the same number density function as another potential. The rationale behind this will be clarified in the following section.

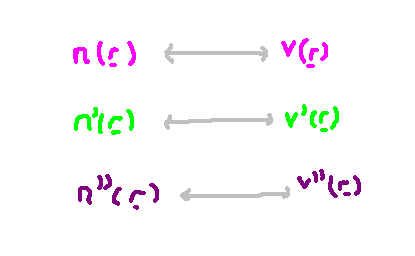
Suppose we have two distinct potentials, labeled ( V ) and ( V' ). These result in two corresponding Hamiltonians, ( H ) and ( H' ), leading to two unique ground states, ( psi ) and ( psi' ). Assuming all other factors remain constant—specifically the interaction and kinetic energy terms—we can formulate a relationship by substituting the old potentials.

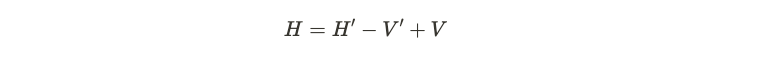
By contracting this relationship with the ground state on both sides, we arrive at the following equation.

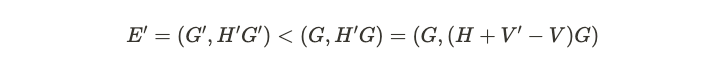
The initial inequality stems from the fact that ( psi' ) is the ground state of ( H' ), while ( psi ) is not, indicating that the energy of ( psi ) exceeds that of ( psi' ). Now, if these Hamiltonians yield identical number densities, we can express this as follows.

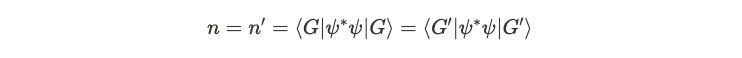
This leads us to the two equations depicted below.

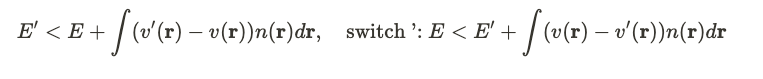
In the second equation, we interchange the primes in the terms, permissible due to the symmetry in the switching process. Adding these two expressions ultimately leads to a contradiction.

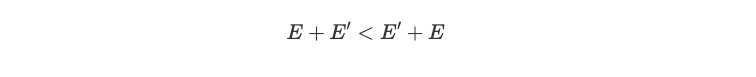
The only incorrect assumption made was that the density functions were equivalent, indicating this cannot hold true. Consequently, for any specified external potential ( v ), we essentially have a distinct density function ( n ). The diagram below illustrates this correspondence.

In this video, "Density Functional Theory, Part 2: Approximations," the speaker elaborates on various approximations used in Density Functional Theory, further clarifying the concepts discussed.

The video titled "Density Functional Theory Part 1/2 (2019)" provides foundational insights into Density Functional Theory, setting the stage for understanding its applications and implications.

References