Chapter 1: The Foundation of the Pythagorean Theorem

The Pythagorean Theorem, expressed as a² + b² = c², is a fundamental concept taught in geometry classes. Most students remember it, but many struggle to grasp why it holds true.

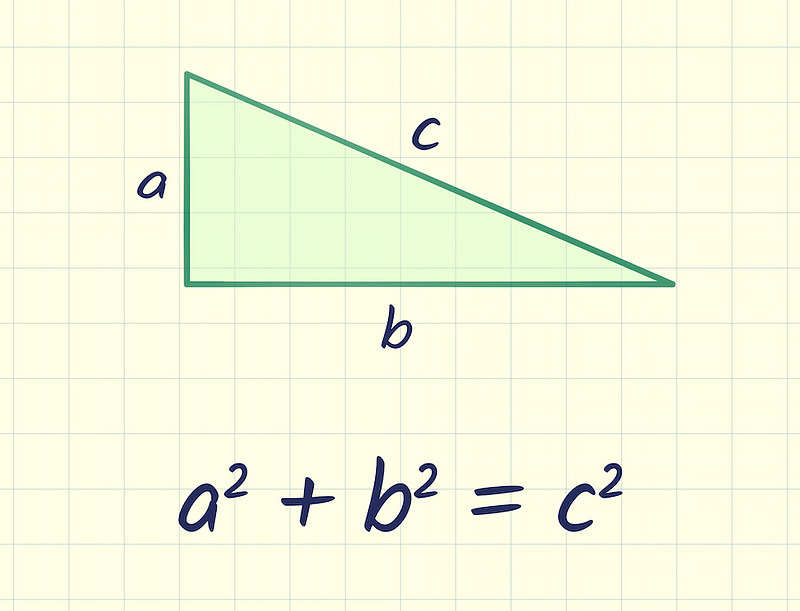
During my school days, I found this theorem easy to memorize, yet I always wished for a deeper understanding of its validity. The standard visual representations often left me confused.

Teachers typically demonstrate the theorem by illustrating squares drawn on the triangle's sides, claiming that the total area of the smaller squares equals the area of the larger square.

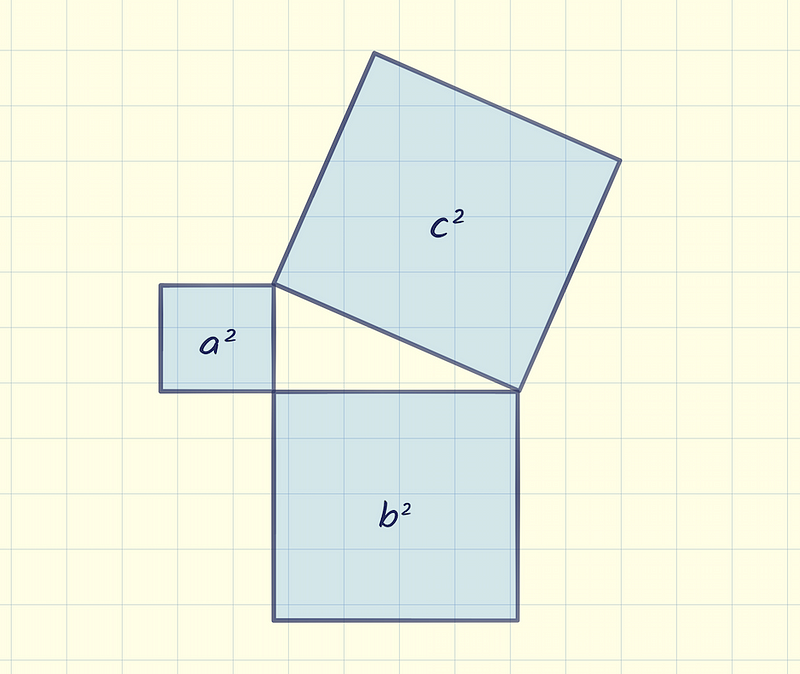
However, these explanations rarely clarified the theorem's truth for me. Even with animations showing the changing dimensions of the triangle, the visual congruence felt unconvincing. While the proportions appeared correct, proving exact equality seemed like an assumption rather than a fact.

Many might argue that teaching proof concepts to middle schoolers is unproductive. In response, I believe that investing time to comprehend a concept is far more valuable than simply memorizing it.

Section 1.1: Establishing What We Know

To affirm the theorem's validity, we must accept certain premises.

• Total Angles: It is a well-known fact that the angles within a triangle sum to 180 degrees. In a right triangle, one angle is 90 degrees, leaving the other two angles to total 90 degrees.

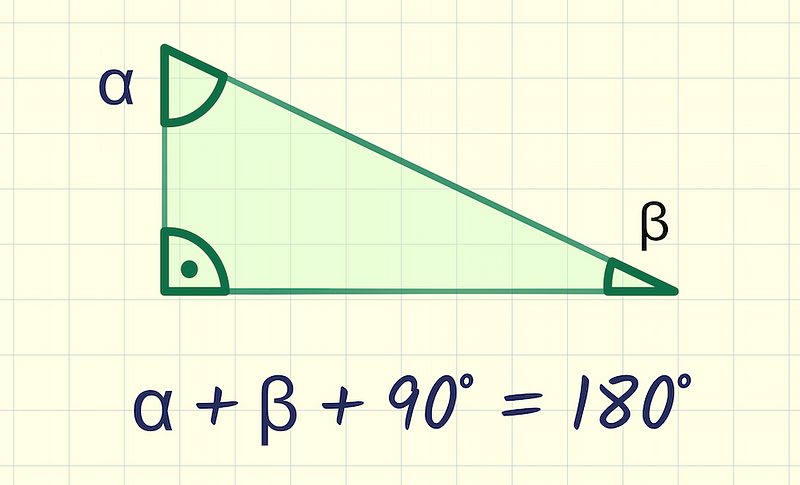
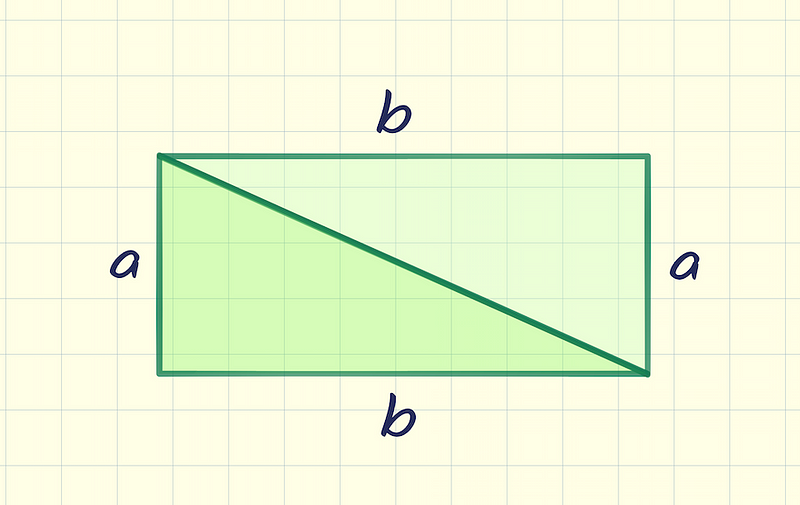
• Area of a Rectangle: A rectangle is defined as a closed shape with four straight sides and right-angled corners. The area of such a rectangle, with sides a and b, is calculated as a × b.
• Area of a Right Triangle: By duplicating and flipping a right triangle, we can form a rectangle. Since the rectangle consists of two identical right triangles, its area is (a × b) / 2.

Section 1.2: Constructing a Square from Right Triangles

Let's return to our right triangle. If we create four identical triangles and arrange them appropriately, we can form a larger square.

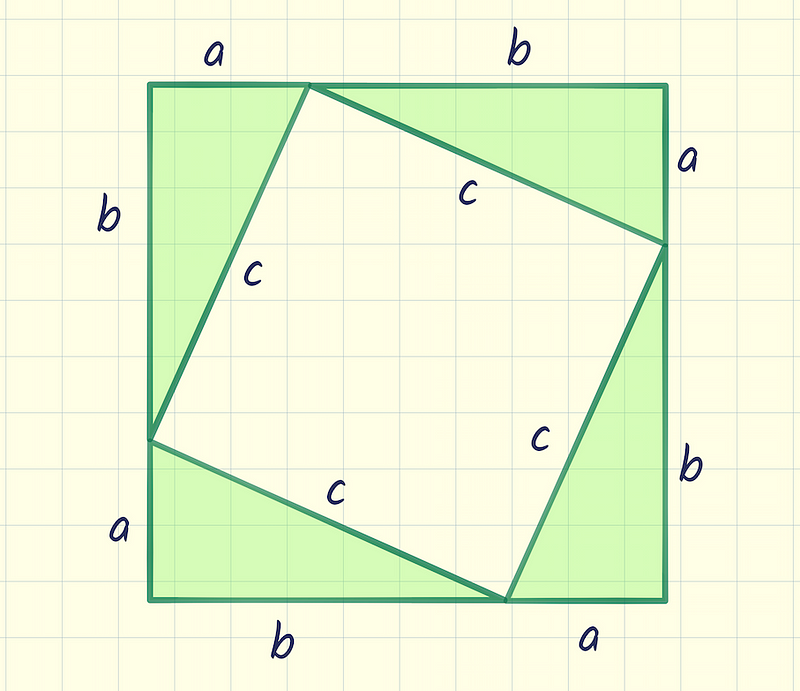
Within this larger square, we can visualize a tilted inner square with a side length of c. To confirm this inner square's legitimacy, we need to analyze its angles.

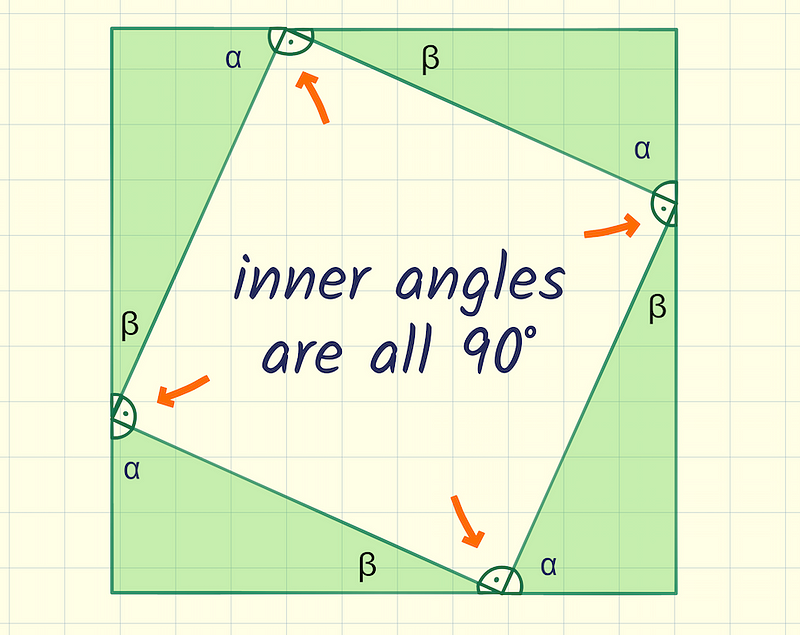
We designed the shape such that the corners with angles α and β meet. Since α + β equals 90 degrees, the remaining angle must also be 90 degrees, confirming that the inner shape is indeed a proper square.

What insights do we gain from this configuration?

• The total area of the outer square can be expressed as (a + b)².
• The area of the inner square is c².
• Each triangle has an area of (a × b) / 2.

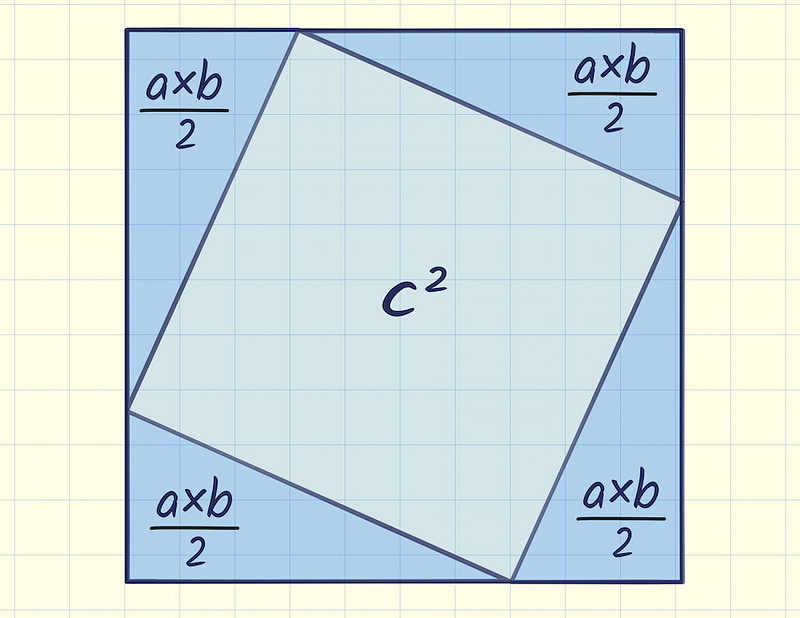
When we combine these observations, we can form an equation: (a + b)² = c² + 4 × ((a × b) / 2). This equation highlights a relationship derived entirely from our constructed figure, emphasizing the equality involving c².

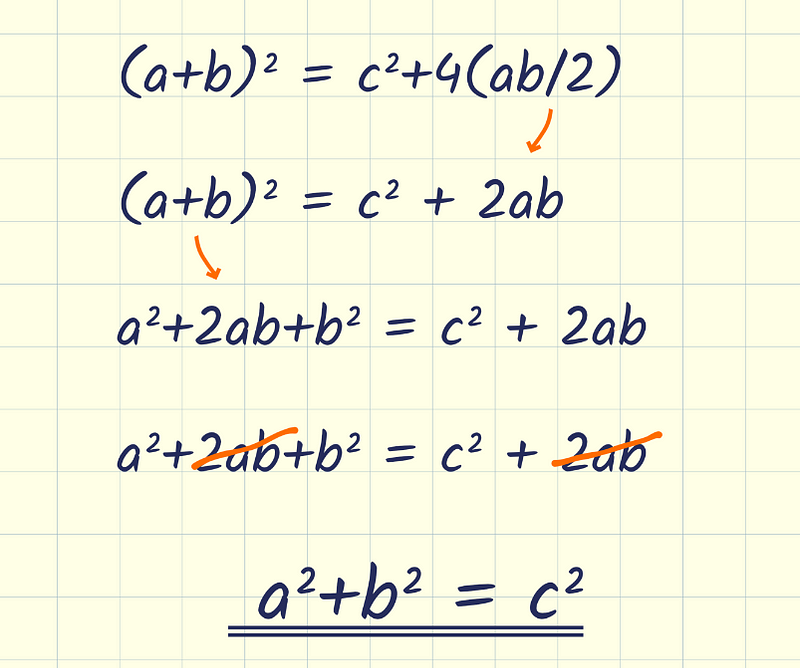
Conclusion: The Significance of the Pythagorean Theorem

Having reached this point, a teacher could confidently explain: “This exceptional relationship in right triangles is known as the Pythagorean Theorem. Tomorrow, we'll explore how it can be utilized to find distances between points in our coordinate system.”

As a 13-year-old, I would have been thrilled to discover such practical applications, envisioning how to implement these concepts in programming to create engaging simulations, like spaceships colliding or moving through space.

This video titled "Why does the Pythagorean Theorem Work?" provides an insightful look into the theorem and its proofs, helping to clarify its significance.

In the video "Pythagorean theorem - Why does a²+b²=c²?", the relationship between the sides of a right triangle is explored further, enhancing your understanding of this mathematical principle.