Dividing the Winnings: Analyzing Probability in Games of Chance
Written on
Chapter 1: The Coin Flip Dilemma
Imagine a scenario where two players, Andy and Beth, engage in a coin-flipping competition with a $100 prize at stake. This isn't merely a game; it serves as a fascinating exploration of probability and fairness. As they flip coins, Andy manages to get four heads, while Beth achieves seven before their math class interrupts. Faced with the need to leave, how do they fairly split the prize?
This question originates from a textbook used in a statistics course where I serve as a teaching assistant. I received numerous inquiries from students seeking clarity on the author's intent. This problem delves deeply into the principles of probability and decision-making amidst uncertainty. Here’s a summary of what I shared with the students in response:
The Problem Presented:
Andy and Beth are competing for a $100 prize by flipping a coin, with the first to reach 10 heads declared the winner. However, they must stop immediately, leaving Andy with four heads and Beth with seven. How should they divide the winnings?
As I contemplated this dilemma, several questions emerged:
- What is the core inquiry?
- Why is the question phrased this way?
- Which distribution or formula is relevant?
- Why can't they simply finish or restart the game?
This situation transcends mere mathematics; it reflects the choices we make and their consequences.
The Mathematical Framework
The textbook suggests a solution grounded in probability theory:

Andy requires six additional heads, while Beth only needs three. The game concludes when one player reaches ten heads, and there could be a maximum of eight more flips left (6 + 3 - 1).
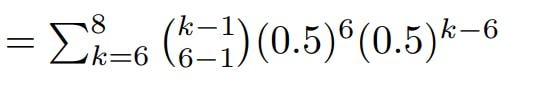
The textbook computes Andy's odds over 6, 7, or 8 flips, utilizing the negative binomial distribution. But does this cover the entire scenario?
Challenging the Assumptions
The flaw lies in the assumptions made; we lack clarity on who will flip next. The complexity of the situation isn't captured by a simple win/lose model. What does fairness mean here?
Revisiting the Inquiry
Let’s reconsider the question. Suppose we explore various scenarios that reveal the true nature of probability distributions.
Negative Binomial Distribution: A Quest for Treasure
Imagine an archaeologist searching for a hidden treasure while navigating ancient traps, each with a 1/3 chance of activation. She must deactivate five traps without triggering any before her time runs out—she only has 15 attempts before the cave collapses.
What’s the probability she secures the treasure on her 10th attempt? What are her chances of escaping unscathed? If she activates a trap, she must restart her attempts.
To tackle this, we can simulate the situation using R to visualize the outcomes.
For part (a), we determine the probability of the archaeologist succeeding on her 10th attempt, which requires four successful deactivations in the first nine attempts, followed by success on the 10th. Using the dnbinom function in R helps us calculate this probability.
For part (b), we need to consider the total of 15 attempts to deactivate five traps, summing the probabilities for success on the 5th through 15th attempts.
For part (c), we’ll analyze the distribution of resets the archaeologist experiences before successfully navigating all five traps. This could resemble a meta-negative binomial scenario, simulated by tracking resets across numerous trials.
- Probability of securing the treasure on exactly the 10th attempt: 8.54%
p_safe <- 2/3
r_successes <- 5
prob_exactly10_att <- dnbinom(
r_success - 1,
size = r_success - 1,
prob = p_safe
)
- Probability of securing the treasure within 15 attempts: 99.82%
max_fail_before_success <- 15 - r_successes
prob_within_15 <- pnbinom(
max_failures_before_success,
size = r_successes,
prob = p_safe
)
- Distribution of trap activations before escaping with the treasure:
# Distribution for 0 to 10 triggers
Hypergeometric Distribution: Alien Invasion
Now, picture Earth under alien attack with 20 spacecraft. A team of pilots, each with a 1/5 success rate, is dispatched. If 10 pilots are sent out, what’s the probability exactly 3 ships are destroyed? How does this change if each pilot’s success rate increases to 1/3?
This scenario employs the hypergeometric distribution since we sample without replacement from a limited group of alien ships.
- Number of successful attempts (k): 3
Number of successful ships (m): 4
Population size (N): 20
Sample size (n): 10
To find the probability for part (a):
N <- 20 # Total alien ships
n <- 10 # Number of pilots
m <- N / 5 # Potentially takedown ships
k <- 3 # Desired successes
prob_exactly_3 <- dhyper(k, m, N - m, n)
For part (b), when each pilot's skill improves to a 1/3 success rate, we adjust m and recalculate the probabilities.
Multinomial Distribution: The Alchemist’s Experiment
An alchemist aspires to transmute lead into gold, silver, or diamond through a mystical process, with specific probabilities for each outcome. After 12 attempts, what’s the probability that he obtains 4 gold, 3 silver, 2 diamonds, and 3 failures?
This scenario is modeled using the multinomial distribution, akin to rolling a four-sided die with different outcomes.
To calculate this, we use:
probabilities <- c(0.2, 0.3, 0.1, 0.4) # Probabilities for each outcome
outcomes <- c(4, 3, 2, 3) # Desired outcomes
prob_exact_distribution <- dmultinom(outcomes, prob = probabilities)
Geometric Distribution: The Hacker’s Dilemma
Envision a hacker attempting to breach a security system that locks after three failed attempts, with a 30% success rate. To avoid locking out, the hacker disconnects after two failed tries. What’s the probability of guessing the password correctly before a third disconnection?
This situation can be analyzed using the geometric distribution.
To find the probability of success within one block of two attempts:
prob_success_on_attempt <- 0.3
prob_failure_on_attempt <- 1 - prob_success_on_attempt
prob_success_in_one_block <- prob_success_on_attempt + (prob_failure_on_attempt * prob_success_on_attempt)
# The probability of at least one success in three blocks
prob_at_least_one_success <- 1 - pgeom(2, prob_success_in_one_block)
Conclusion
Probability transcends mere calculations; it offers insight into our world. From splitting prizes to seeking treasures or defending against invaders, it equips us to navigate life's uncertainties. Let’s embrace and apply this knowledge as we play the intricate game of chance that is life.
If you find value in this, consider supporting my work with a coffee!
Eddie Coda
Gratefully accepting your gesture of kindness. Perhaps a pastry as well?
www.buymeacoffee.com
Video Description: This video discusses the probability theory behind dividing stakes in interrupted games, providing a deeper understanding of the concepts involved.
Video Description: Explore how a gambler must manage their bets in a game with multiple outcomes, highlighting the complexities of probability in real scenarios.