Chapter 1: The Fundamental Rule of Negatives

In the realm of mathematics, one of the earliest lessons we encounter is that "multiplying a negative number by another negative number yields a positive number." This principle is often repeated to the point where it feels like a fundamental truth ingrained in our minds. However, the reasoning behind this rule is not typically explored until higher education, such as college.

Many of us might have our own interpretations or justifications for this rule. I can recall a teacher explaining that multiplying negatives is akin to flipping from positive to negative and then back to positive on a number line.

For the sake of clarity, let’s refer to the statement "a negative number times a negative number is a positive number" as the claim. But what if I told you that this claim didn’t have to hold true? Imagine if multiplying two negative numbers resulted in a negative value instead. This idea might seem counterintuitive, as it contradicts a deeply-rooted belief. However, it’s essential to understand that this belief is based on a choice made within the framework of mathematics.

Mathematics operates on a set of chosen axioms, which are rules we must adhere to. These axioms and the structures we derive from them lead us to accept the claim as true.

Now, rather than delving into all the axioms, let’s focus on a structure you’ve been using since you started counting on your fingers, which is fundamental to all mathematics today. This structure is known as a ring. You might not have encountered the term "ring" before, but think of it as a set, typically denoted as R, that meets certain criteria allowing us to perform addition (+) and multiplication (×). A prime example of a ring is the set of integers.

Let’s consider one property of a ring: the distributive property. Specifically, if R is a ring, for any three elements a, b, and c in R, we have the equation a × (b+c) = (a × b) + (a × c).

You may not be familiar with rings or related concepts like groups or fields, but these structures enable us to perform the calculations we often take for granted. For instance, since integers form a ring, we can be confident that adding or multiplying any two integers will always yield another integer. While this may seem obvious, it’s a conclusion reached because of the properties of rings.

Additionally, because integers form a ring, we know that for every element a, there exists an inverse element -a such that (a) + (-a) = 0. This is not the case for natural numbers, as there’s no natural number that can be added to 4 to cancel it out, indicating why natural numbers do not form a ring.

In essence, knowing that a set forms a ring ensures that we won’t encounter any unexpected outcomes. Consider how much more complicated arithmetic would be if we couldn't be certain that for any a and b in the ring, a ± b remains in the ring.

Now, let’s return to the core question: why does it make more sense to conclude that multiplying a negative number by another negative number results in a positive? As mentioned earlier, the distributive property is crucial.

We can start with the equation: 3 × (5–5) = 3 × 0 = 0.

Using the distributive property, we can express it as: 3 × (5–5) = (3 × 5) + (3 × (-5)).

For this to hold true, we conclude: (3 × 5) + (3 × (-5)) = 0.

Given that it’s clear 3 × 5 > 0, it follows that 3 × (-5) must be < 0. Thus, we’ve demonstrated that for the distributive property to remain valid, a positive number multiplied by a negative number must yield a negative result.

This logic can be extended further: Let a and b be positive. Thus, 0 = a × (0) = a × (b-b) = (a × b) + (a × (-b)), indicating that since a × b > 0, we must have a × (-b) < 0.

We can also prove similarly that since (-3) × (5–5) = 0, it follows that ((-3) × 5) + ((-3) × (-5)) = 0. From our earlier reasoning, (-3) × 5 < 0, which implies that for the distributive property to hold, (-3) × (-5) must be > 0.

By formalizing this proof, we conclude that if we accept that the properties of a ring are valid, then we must also accept that multiplying two negative numbers yields a positive result.

Let’s finish with a geometric approach to justify this claim. Consider the following reasoning: 100 = 10 × 10 = (11–1) × (11–1) = 121 - 11 - 11 + ((-1) × (-1)) = 99 + ((-1) × (-1)), thus leading to the conclusion that ((-1) × (-1)) = 1 > 0.

To visualize this, let’s look at a rectangle:

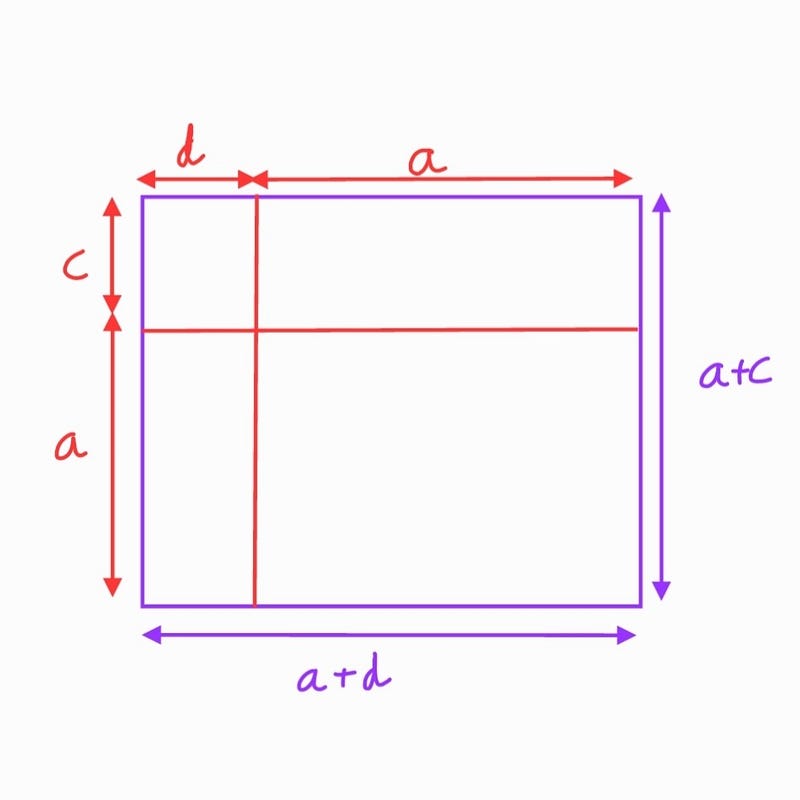
It's evident from the diagram that: a² = (a+c)(a+d) - (a+d)(c) - (a+c)(d) + (c)(d). Alternatively, it can be expressed algebraically as: a² = ((a+c)-c)((a+d)-d) = (a+c)(a+d) - (a+d)(c) - (a+c)(d) + (-c)(-d).

This comparison shows that: cd = (-c)(-d).

Thus, we’ve explored several perspectives on why multiplying two negative numbers results in a positive outcome. I hope this has provided you with some new insights, and if you have additional justifications for this claim, please feel free to share.

Thank you for reading. This article was inspired by a reader's email, and I appreciate their contribution.

If you found this article helpful, consider following me and my publication, Y(Math), to help spread my work to a broader audience. You can also support me and other writers you enjoy by joining Medium through my referral link.

Chapter 2: Video Insights on Negative Multiplication

The first video explains the concept of why a negative times a negative results in a positive outcome, providing visual and mathematical insights.

The second video further explores the reasoning behind the negative times negative equals positive rule, presented in an engaging and educational manner.