Chapter 1: The Concept of Planar Graphs

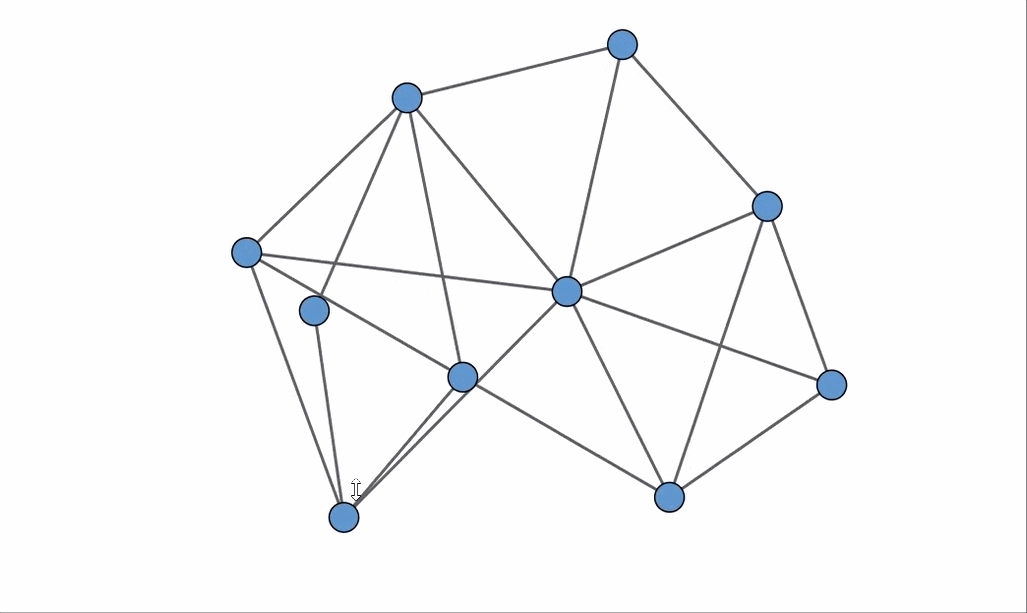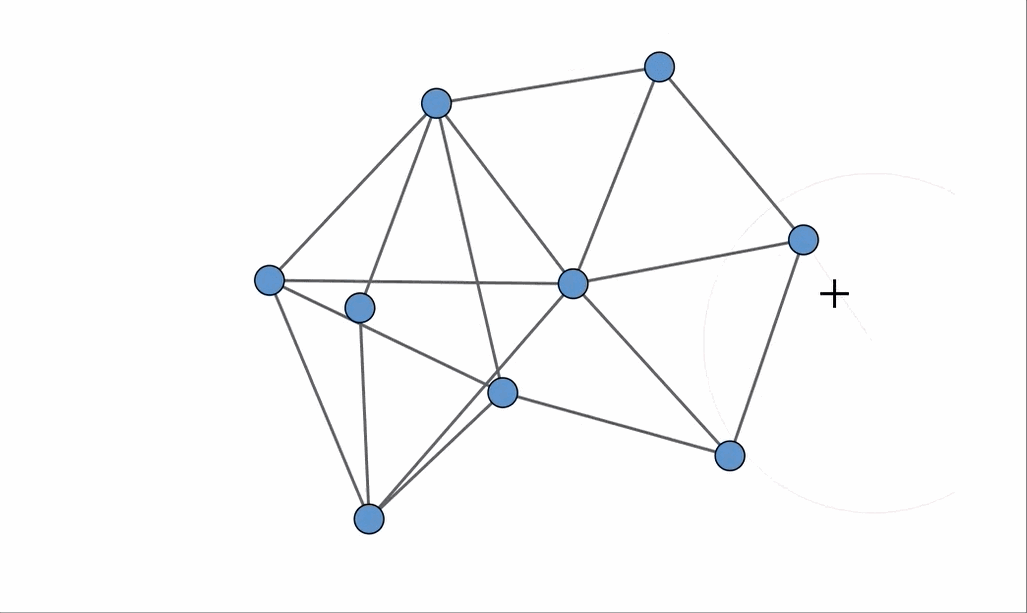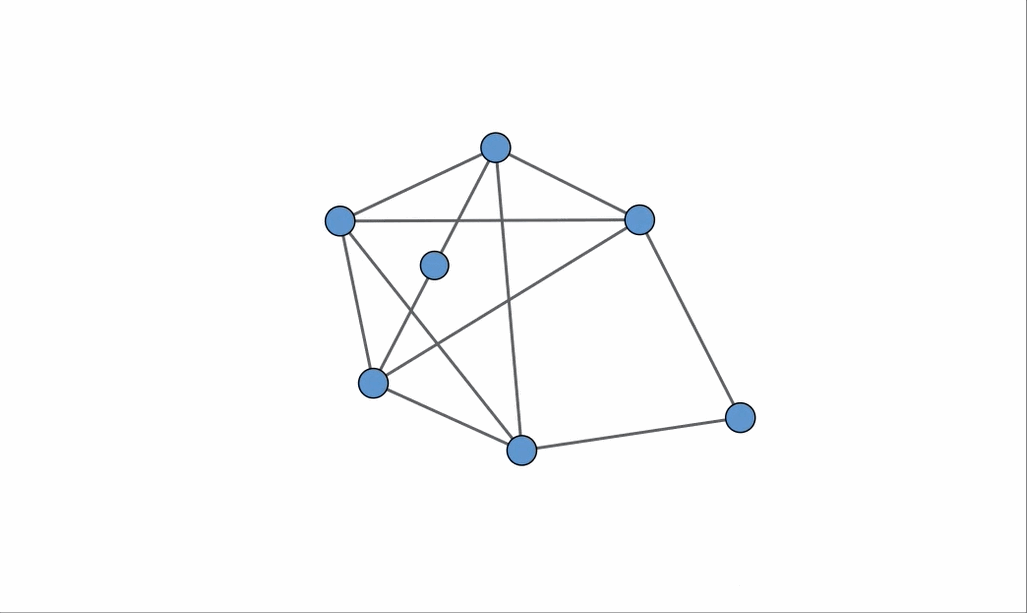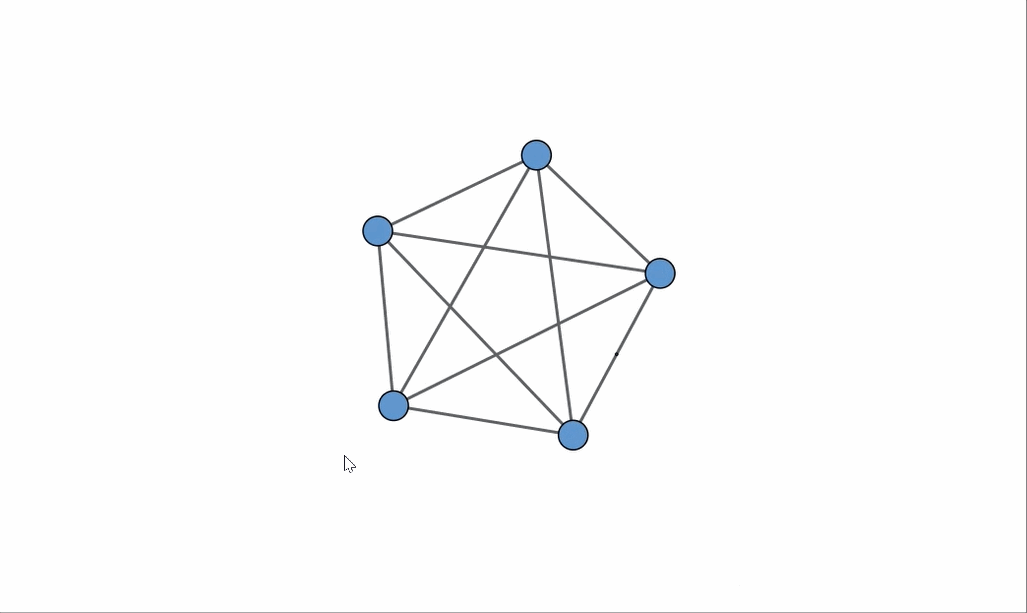
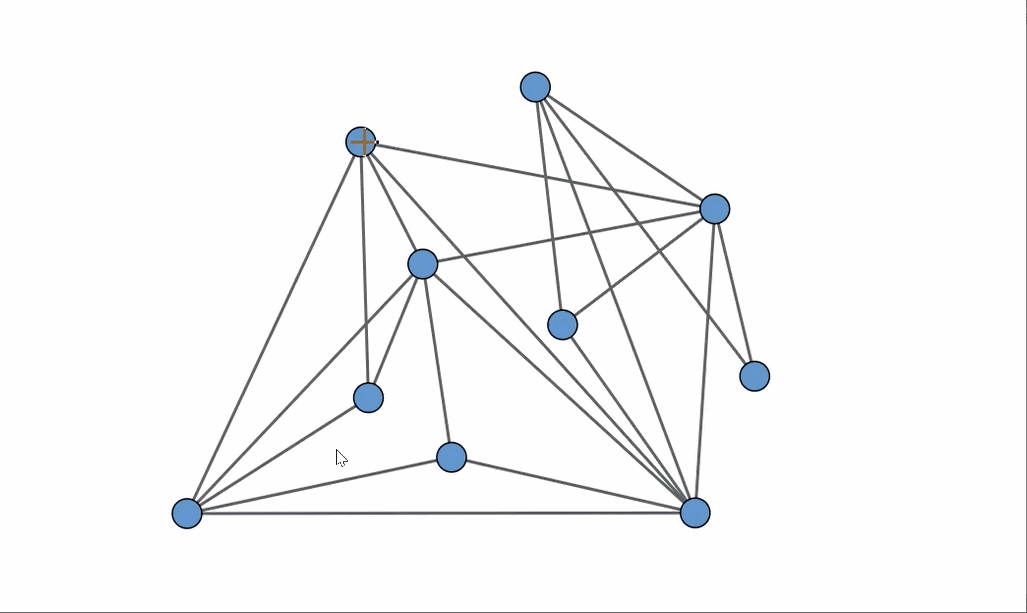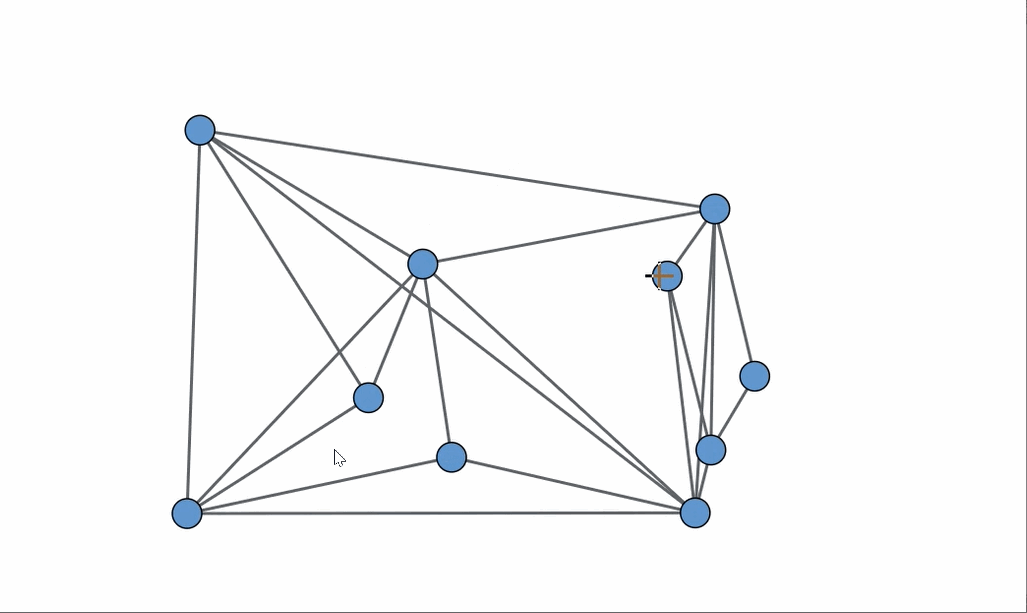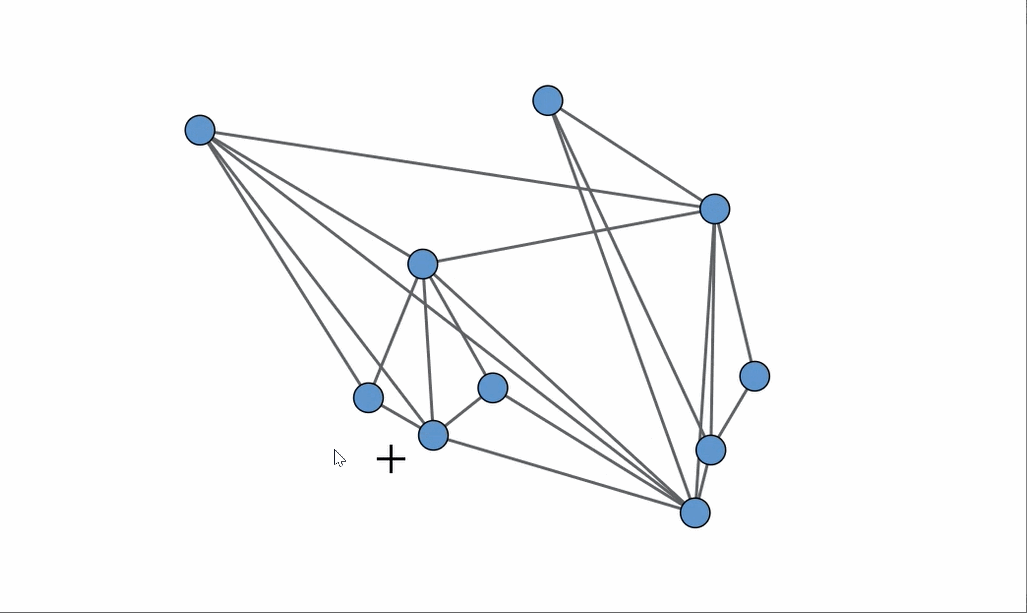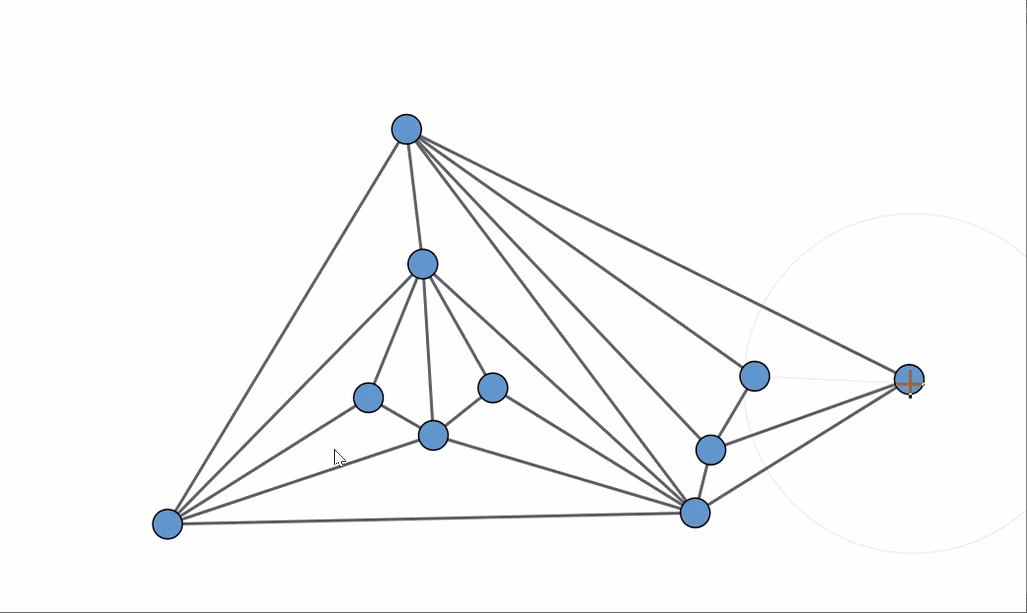
Identifying a planar graph can be surprisingly challenging. A planar graph is defined as one that can be represented on a two-dimensional plane without any of its edges overlapping. In the illustration displayed above, only one of the three presented graphs qualifies as planar. However, discerning which one it is may not be as straightforward as it seems!

To clarify, let’s examine the graph located in the bottom left corner. We can demonstrate that this graph is non-planar by removing certain vertices and contracting specific edges, revealing that it contains K5, which is the complete graph with five vertices.

K5 is inherently non-planar, and any graph that can be simplified to K5 by removing vertices or edges, or by contracting edges, is also non-planar. Contracting an edge involves merging a vertex with its two adjacent vertices into a single edge.

This principle extends to K3,3 as well (the complete bipartite graph consisting of two sets of three vertices). Any graph that can be transformed into K3,3 through similar reductions is classified as non-planar. Furthermore, every non-planar graph can ultimately be reduced to either K5 or K3,3! This fascinating relationship is encapsulated in Kuratowski’s Theorem (also referred to as Wagner’s Theorem). For a deeper dive into this topic, refer to the article linked below.

The first video, titled "Which Complete Graphs are Planar? | Graph Theory," provides an insightful exploration into the characteristics of planar graphs and the underlying principles that govern their identification.

Chapter 2: Unveiling Non-Planarity

As we delve deeper, let’s consider an animation that illustrates how K3,3 is concealed within the graph in the bottom right, thereby validating its classification as non-planar.

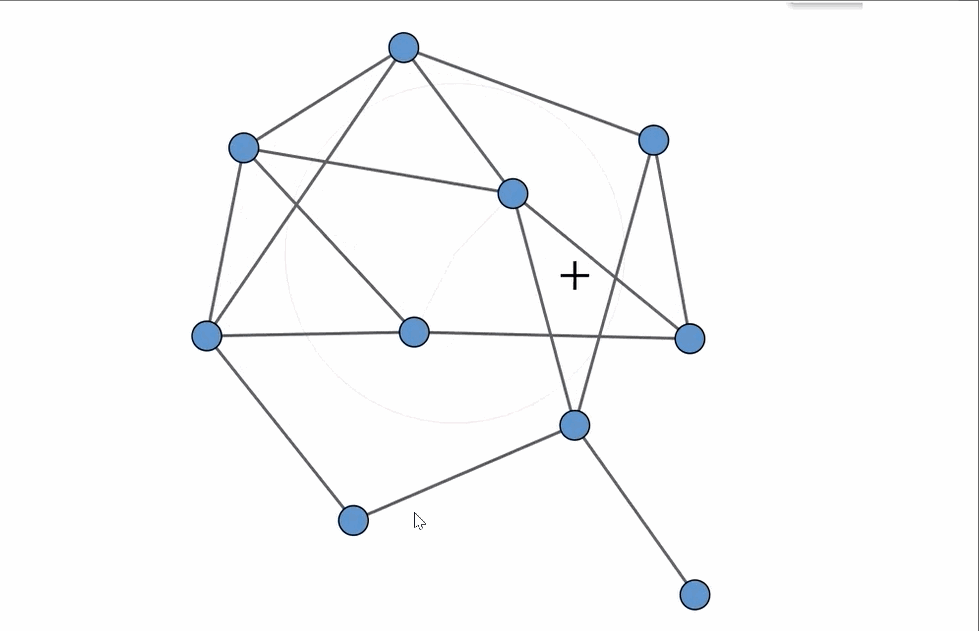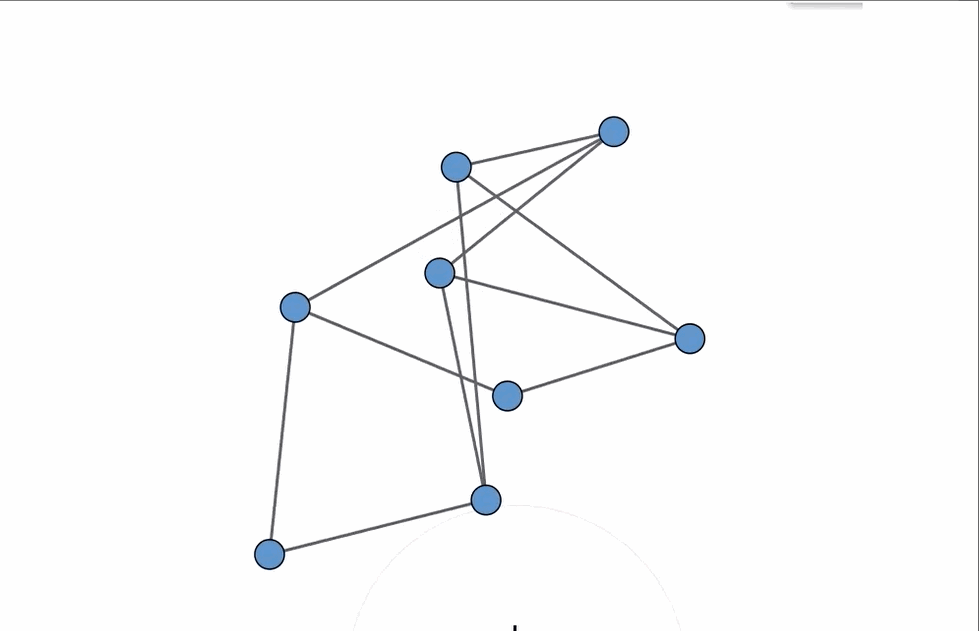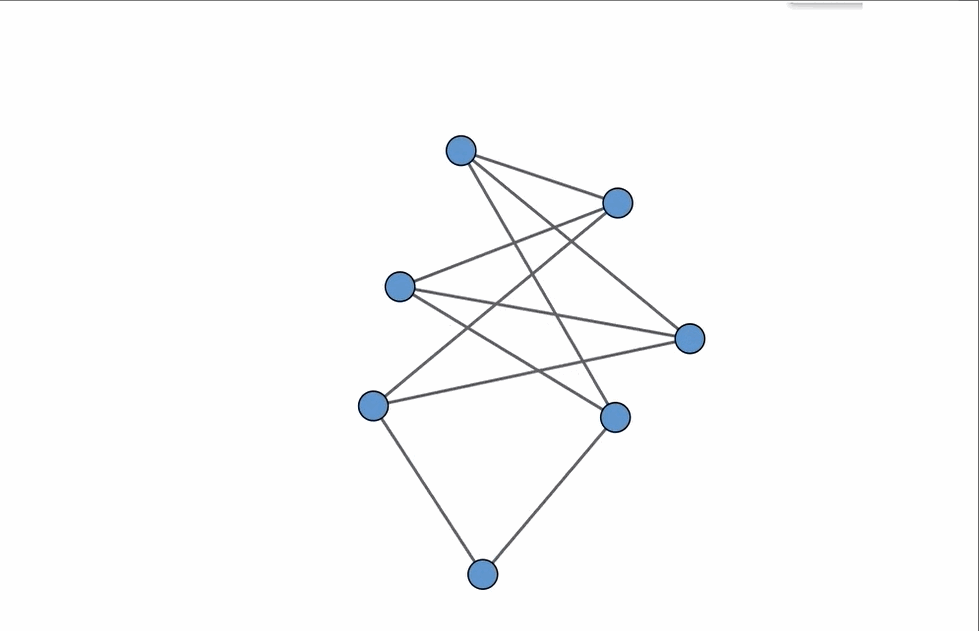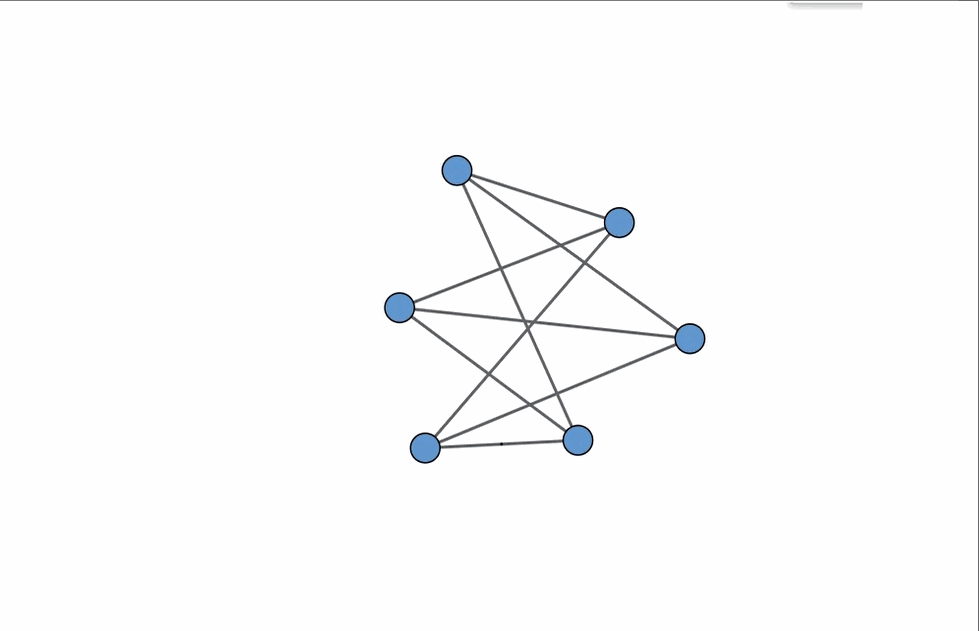
Now, returning to the original set of graphs, the one that is indeed planar is the one located in the upper right corner, which, interestingly, has the most edges! An animation showcasing a rearrangement of the vertices provides a clear example of how to achieve a planar embedding.

Who would have imagined this outcome? Did you manage to guess correctly?

The second video, "CG11 Which Graphs are Planar?" offers an intuitive explanation of Kuratowski’s and Wagner’s Theorems, complete with numerous diagrams that enhance understanding.