Discovering Pi: An Unconventional Approach to Approximation
Written on
Chapter 1: Understanding Pi
When asked to define Pi, most people would respond with the classic description: it represents the ratio of a circle's circumference to its diameter. You would be absolutely correct. The significance of Pi is closely linked to circles and trigonometric functions, leading one to assume that its mathematical applications are largely confined to these areas. However, the experiment we're about to conduct appears to have no direct correlation to circles or trigonometry, yet it can still yield an approximation of Pi—a truly astonishing result!
The Experiment
To embark on this experiment, gather the following items: a pen, paper, a ruler, and several matches.
- Measure the length of a match or needle, which we will denote as x.
- Draw parallel lines on your paper, ensuring that the spacing between each pair of lines is consistent, denoting this distance as t.
- Count the number of matches or needles you have, referred to as n.
- Randomly drop the matches onto the paper.
Having completed these steps, you now have a means to approximate Pi. It may seem surprisingly straightforward, but let’s delve deeper into where Pi may be concealed.
As you observe the matches that have landed, you'll notice that some intersect with the drawn lines while others do not. Count the number of matches that cross any of the lines; we will call this value k. After noting all the necessary parameters, use the following formula to make your approximation:
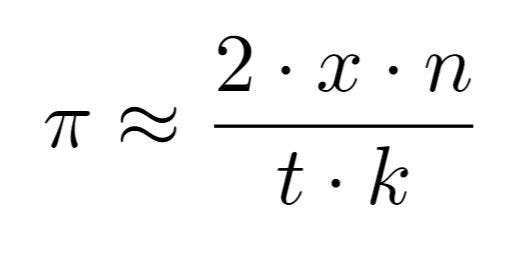
The accuracy of your approximation may fluctuate based on the number of matches you drop. To enhance the precision of your results, consider increasing the number of matches and conducting the experiment again. Below, you can view a simulation created by SamuelHunter.
Video Description: This video demonstrates an engaging method to approximate Pi using a needle-throwing experiment, offering insights into the underlying mathematics.
Final Thoughts
The experiment we've explored falls under the category of Monte Carlo experiments, which utilize repeated random sampling to achieve numerical outcomes. The specific challenge we tackled is known as Buffon's needle problem. Initially, this problem was not intended to approximate Pi but aimed to determine the probability of a match landing on a line.
Video Description: This video delves into the fascinating connection between probability and Pi through Buffon’s needle problem, revealing surprising insights.