Exploring Integer Solutions: A Mathematical Journey
Written on
Chapter 1: Introduction to the Problem
Recently, a reader posed a thought-provoking mathematical challenge related to one of my earlier articles. The task is to identify all integers x>3 and y>0 that satisfy the equation:
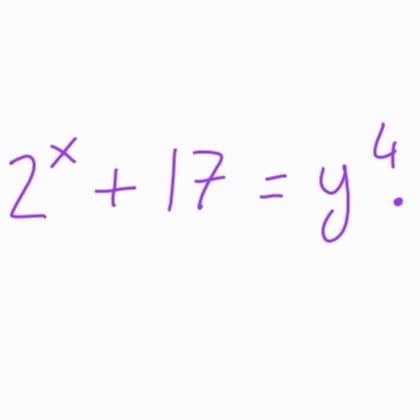
After several months, I decided to tackle this problem and have come up with three distinct solutions. I believe there are potentially more methods, and I encourage others to share their findings. The solutions I present range from simple to complex, illustrating the significance of foundational number theory knowledge.
Section 1.1: Solution 1 – Applying Fermat’s Little Theorem
Upon analyzing the problem, my first instinct was to utilize Fermat’s Little Theorem (FLT). Recall that FLT states that for a prime number p and an integer a that is not divisible by p (meaning a and p are coprime), the following holds:
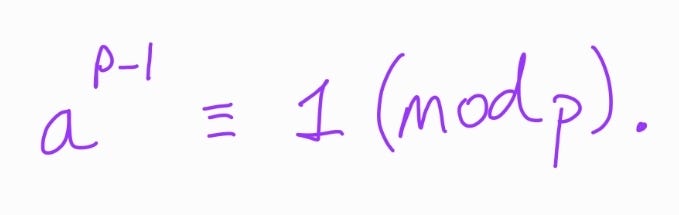
The only limitation in using FLT arises when y is a multiple of 17. However, this scenario is impossible because it implies that 2^x would also be a multiple of 17, which is clearly not the case. We will demonstrate this explicitly in our second solution.
Applying FLT, we derive:
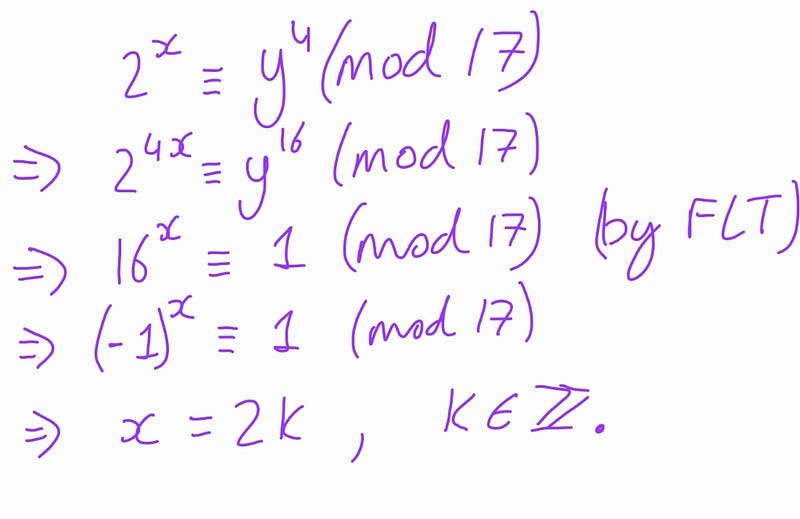
For those less familiar with number theory, the calculations above may seem a bit perplexing. This confusion is understandable, as we employed modular arithmetic, a fundamental concept encountered early in number theory studies. The key takeaway here is that we can swiftly conclude that x=2k for some integer k. In the next solution, we will bypass modular arithmetic and work a bit harder to reach the same conclusion.
Now, returning to the original equation, we can rewrite it as follows:
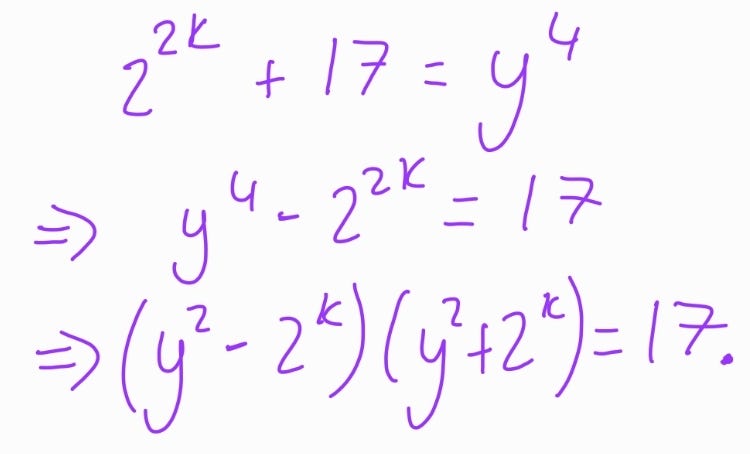
Given that 17 is prime, we can ascertain that:
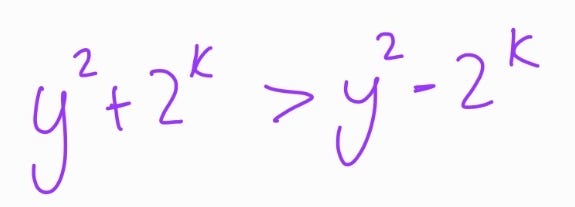
Consequently, we can conclude that our equation yields the unique solution (x,y) = (6,3).
Section 1.2: Solution 2 – Remainder Comparisons
In this approach, we again utilize modular arithmetic, but this time we will focus on comparing remainders rather than applying FLT directly. We start with the observation that:
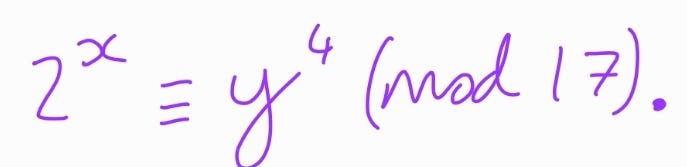
Next, we compute the remainders for both sides of the equation to determine when they can be equal:


By examining the remainders, we can clarify which values satisfy our equation:
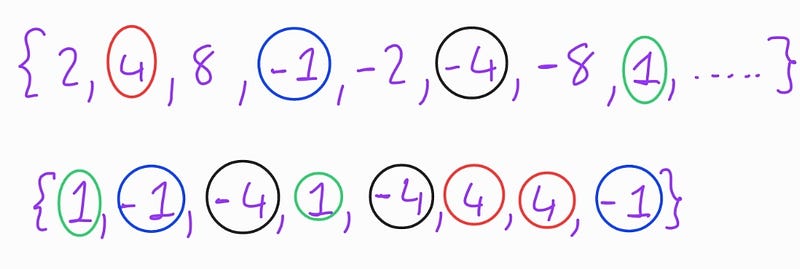
It is crucial to note that only every second value from the left side's remainders matches those from the right side. Therefore, a solution is only possible if x is even, confirming that x=2k for some integer k, just as found in Solution 1. We can then complete this solution similarly to the previous one.
Chapter 2: Solution 3 – Basic Algebra Approach
For this final solution, we will employ basic algebra. There are various ways to approach this, but I will illustrate my method through the properties of even and odd number multiplication.
To begin, we can re-express our equation as follows:
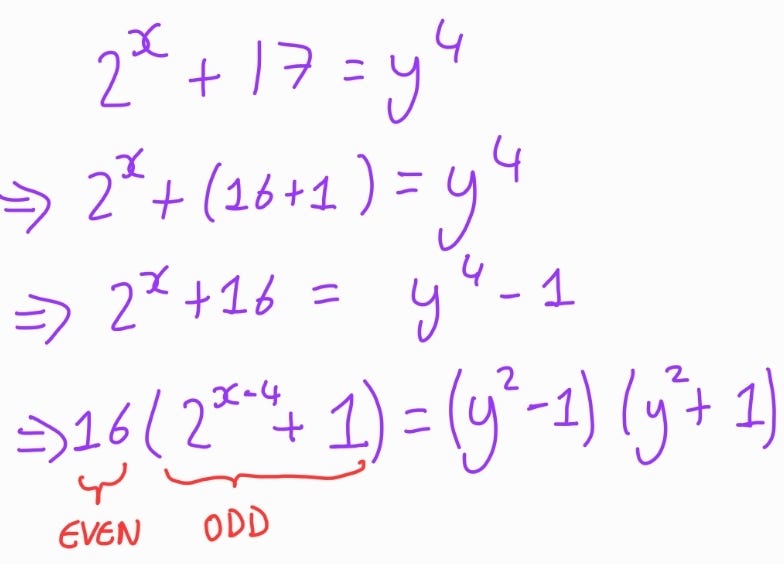
From here, we can deduce that y²-1 and y²+1 are both even, and since they share a common factor of 2, one must be divisible by 8 while the other is divisible by 2. Additionally, the odd factor on the left side must divide either y²-1 or y²+1, leading us to four cases to explore.
Case 1:
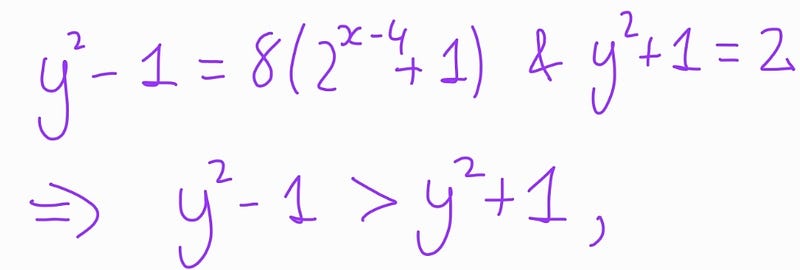
This case yields no solutions.
Case 2:
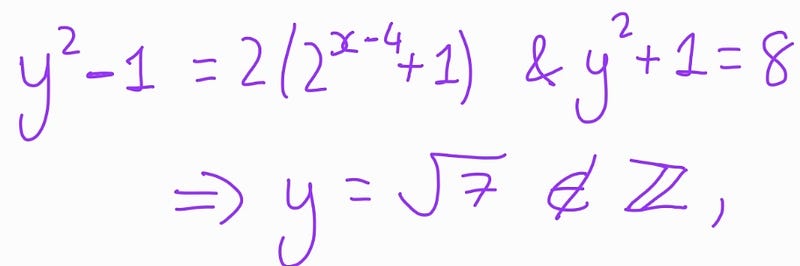
Similarly, this case does not provide a valid solution.
Case 3:
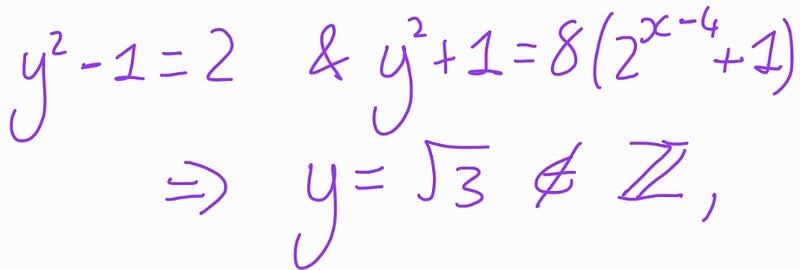
Again, no solutions arise from this case.
Case 4:
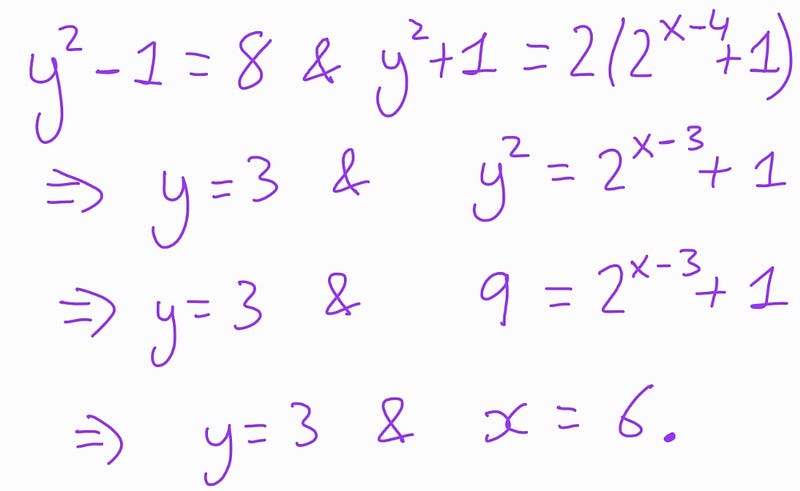
Thus, we arrive at the same unique solution (x,y) = (6,3), confirming our previous findings. While this solution required the least technical expertise, it demanded a clever application of basic principles.
If anyone has alternative intriguing solutions, I would be delighted to hear them! Thank you for reading, and I extend my gratitude to Bogumił Kamiński for proposing this captivating problem.
For those interested, consider following my publication Y(Math) to help broaden the reach of my articles. You can also join Medium using my referral link to support me and other writers whose work you enjoy.