Unraveling Infinitesimal Symmetries and Noether’s Theorem
Written on
Chapter 1: Introduction to Infinitesimal Symmetries
In my last entry, I delved into the fascinating Noether’s theorem. This theorem provides a powerful method for deriving conserved quantities from the symmetries present in a physical system. In this post, I aim to elaborate on the mechanics behind this process. Imagine we identify a transformation that preserves the physical characteristics of a system. According to Noether’s theorem, these transformations lead to the creation of Noether currents.
Moreover, Noether currents adhere to specific conservation principles, possessing distinct characteristics. They cannot exhibit 'generative' or 'destructive' features, a topic I will clarify further in the subsequent section. Consequently, we utilize these currents to formulate conserved quantities, such as electric charge or energy.
Section 1.1: The Role of Continuous Symmetries
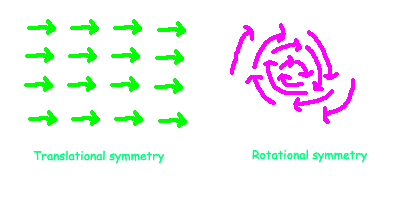
How do we derive a Noether current? Notably, Noether’s theorem applies exclusively to continuous symmetries—transformations that are smooth and gradual. When a symmetry transformation is smooth, it allows for a slight adjustment in the direction of that symmetry. In contrast, for discontinuous symmetries, such as reflection, the concept of a 'nudge' becomes ambiguous.
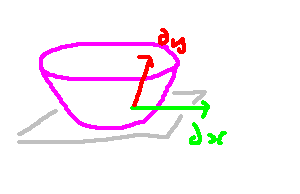
For instance, if a system demonstrates rotational symmetry, a minor adjustment would entail a rotation by a small angle. Similarly, for translational symmetry, one might apply a slight shift in the x-direction. Generally, when we deal with fields or particles, we can implement this small adjustment to obtain a new, slightly altered field or particle. This operation is referred to as a perturbation and is typically represented by the Greek letter delta (δ).
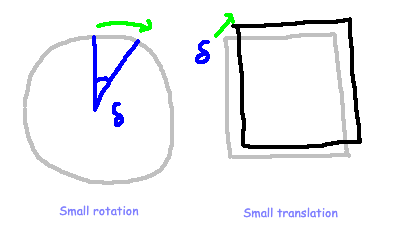
The above diagram illustrates how a minor rotation or translation might manifest when applied to basic shapes. We can extend these transformations to fields as well. For example, consider a field where, at every spatial point, the field aligns in the x-direction; this scenario indicates x-translational symmetry. Conversely, envision a field that rotates around the origin, displaying rotational symmetry.
Mathematically, we can express a minor transformation through the equation below. Here, the Greek letter phi (φ) symbolizes the field itself, while the arrow signifies a 'mapping.' The left side of the arrow depicts the field prior to the transformation, and the right side reflects its state afterward.
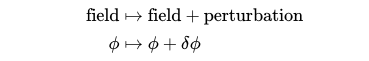
Section 1.2: Understanding the Lagrangian
In most physical models, the Lagrangian primarily depends on two factors: the field's value and its derivative. In a relativistic context, the field's derivative indicates how it varies across space and time, comprising four components. The first component addresses time variation, while the last three correspond to changes in the x, y, and z directions, respectively. This derivative is represented by a mathematical construct known as a vector.
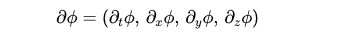
The curly symbols with subscripts denote the rate of field change over time and in the x-direction. The curly notations represent partial derivatives, capturing the field's variation in specific directions. This gradient across various axes is depicted in the diagram below.
In more complex physics models, the Lagrangian could theoretically depend on time or space. The equation below illustrates that the Lagrangian is a function of these variables.
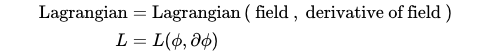
Thus, the Lagrangian's value is contingent upon these fields, suggesting it will vary when the field values change. Consequently, a perturbation in the fields should result in a corresponding shift in the Lagrangian's value, represented by a small delta.
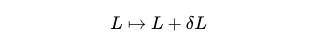
If the transformation qualifies as a symmetry of the Lagrangian, then the alteration in its value should be zero! As mentioned in my previous post, Lagrangians are equivalent up to a total derivative term. Therefore, if the transformed Lagrangian only differs by a total derivative term, it is deemed a symmetry.
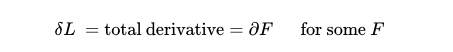
Chapter 2: Video Insights on Infinitesimal Symmetries
This video titled "Week 11 Clip 8 - Infinitesimal symmetries: Lie derivative" provides a detailed exploration of infinitesimal symmetries and how they relate to Noether's theorem.
The second video, "Generic symmetry-forced infinitesimal rigidity: translations and rotations," delves into the mechanics of symmetry-induced rigidity and its applications in physics.