Finding the Value of a: An Engaging Algebra Challenge
Written on
Chapter 1: Introduction to the Puzzle
In this engaging algebra puzzle, we have five unit squares positioned within a coordinate plane, starting from the origin. A diagonal line runs from the point (a, 0) to (3, 3), effectively splitting the total area into two equal parts. The question arises: What is the value of a?
Before you proceed, I encourage you to pause for a moment, grab some pen and paper, and give this a try. Once you're ready, continue reading to uncover the solution!
Section 1.1: Understanding the Area
Each unit square has a side length of 1, resulting in an area of 1 for each square. Consequently, the total area covered by the five squares is 5. Knowing that the shaded area is half of the total area, we can deduce that it covers an area of 5/2.
Next, let’s take a look at the following diagram for better visualization.
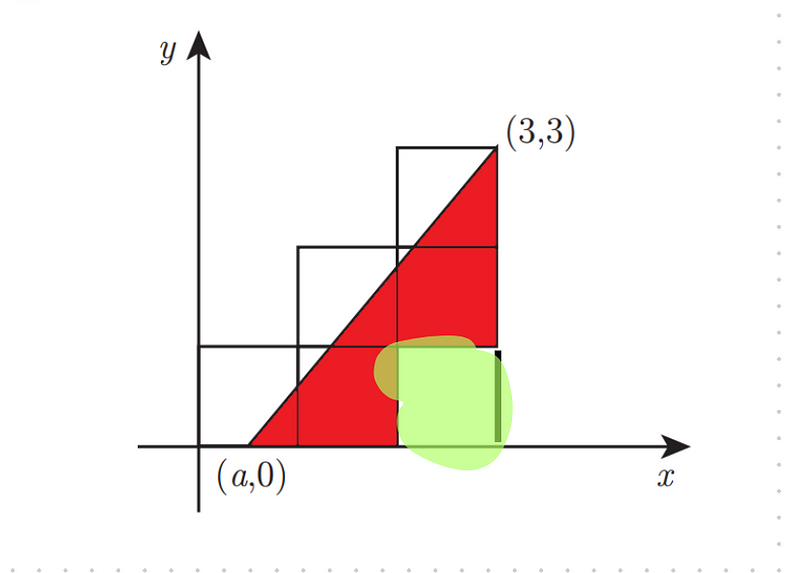
The shaded red region can be conceptualized as a triangle with a base extending from (3 - a) and a height of (3 - 1), corresponding to the area of one unit square.
Let’s apply the formula for the area of a triangle, A = 1/2(b)(h):

Through solving this equation, we find that a = 2/3. And there you have it—our solution!
Section 1.2: Reflection on the Process
What did you think of this problem-solving journey? I would love to hear your thoughts—please share your reflections in the comments section below!
Chapter 2: Further Exploration
The first video titled "How to Find the Mean | Math with Mr. J" provides an insightful look into basic mathematical concepts, which can enhance your understanding of algebraic puzzles.
The second video, "What is a 'Solution Set' for an Equation (Algebra)," dives deeper into algebraic solutions and concepts that could help clarify the problem further.
Thank you for engaging with this puzzle! If you enjoyed it, don’t hesitate to clap for this article. Your support means a lot!
